»ΪΒ»»ΐΫ«–Έ
–‘Ό|(zh®§)ΘΚ
(1)»ΪΒ»»ΐΫ«–ΈΒΡ¨Π(du®§)ëΣ(y®©ng)ΏÖœύΒ»ΓΔ¨Π(du®§)ëΣ(y®©ng)Ϋ«œύΒ»����ΓΘ
(2)»ΪΒ»»ΐΫ«–ΈΒΡ÷ήιL(zh®Θng)œύΒ»���ΓΔΟφΖeœύΒ»���ΓΘ
(3)»ΪΒ»»ΐΫ«–ΈΒΡ¨Π(du®§)ëΣ(y®©ng)ΏÖ…œΒΡ¨Π(du®§)ëΣ(y®©ng)÷–ΨÄ��ΓΔΫ«ΤΫΖ÷ΨÄ�����ΓΔΗΏΨÄΖ÷³eœύΒ»����ΓΘ
»ΪΒ»»ΐΫ«–ΈΒΡ≈–Ε®ΘΚ
ΔΌΏÖΫ«ΏÖΙΪάμ(SAS) ”–É…ΏÖΚΆΥϋ²ÉΒΡäAΫ«¨Π(du®§)ëΣ(y®©ng)œύΒ»ΒΡÉ…²Ä(g®®)»ΐΫ«–Έ»ΪΒ»�����ΓΘ
ΔΎΫ«ΏÖΫ«ΙΪάμ(ASA) ”–É…Ϋ«ΚΆΥϋ²ÉΒΡäAΏÖ¨Π(du®§)ëΣ(y®©ng)œύΒ»ΒΡÉ…²Ä(g®®)»ΐΫ«–Έ»ΪΒ»���ΓΘ
ΔέΆΤ’™(AAS) ”–É…Ϋ«ΚΆΤδ÷–“ΜΫ«ΒΡ¨Π(du®§)ΏÖ¨Π(du®§)ëΣ(y®©ng)œύΒ»ΒΡÉ…²Ä(g®®)»ΐΫ«–Έ»ΪΒ»ΓΘ
ΔήΏÖΏÖΏÖΙΪάμ(SSS) ”–»ΐΏÖ¨Π(du®§)ëΣ(y®©ng)œύΒ»ΒΡÉ…²Ä(g®®)»ΐΫ«–Έ»ΪΒ»��ΓΘ
Δί–±ΏÖ��ΓΔ÷±Ϋ«ΏÖΙΪάμ(HL) ”––±ΏÖΚΆ“Μ½l÷±Ϋ«ΏÖ¨Π(du®§)ëΣ(y®©ng)œύΒ»ΒΡÉ…²Ä(g®®)÷±Ϋ«»ΐΫ«–Έ»ΪΒ»��ΓΘ
ΖΫΖ®Ω²ΫY(ji®Π)ΘΚ
≥ω§F(xi®Λn)É…Β»ΏÖ»ΐΫ«–ΈΓΔÉ…Β»―ϋ÷±Ϋ«»ΐΫ«–ΈΆ®≥Θ”Ο SAS ΉC»ΪΒ»;
Β»―ϋ÷±Ϋ«»ΐΫ«–Έ≥Θ“äίo÷ζΨÄΧμΖ®--ΏBΫY(ji®Π)÷±Ϋ«μîϋc(di®Θn)ΚΆ–±ΏÖ÷–ϋc(di®Θn);
É…÷±Ϋ«»ΐΫ«–ΈΉC»ΪΒ»≥Θ”ΟΖΫΖ®ΘΚSAS,AAS,HL;≥ω§F(xi®Λn)Β»―ϋ÷±Ϋ«»ΐΫ«–ΈΜρ’ΐΖΫ–ΈΩ…Ρή”ΟΒΫ K –Ά»ΪΒ»���ΓΘ
Ϋ«ΤΫΖ÷ΨÄ
–‘Ό|(zh®§)Ε®άμΘΚ
Ϋ«ΤΫΖ÷ΨÄ…œΒΡϋc(di®Θn)ΒΫΫ«É…ΏÖΒΡΨύκxœύΒ»����ΓΘ
≈–Ε®Ε®άμΘΚ
ΒΫΫ«É…²Ä(g®®)ΏÖΨύκxœύΒ»ΒΡϋc(di®Θn)‘ΎΏ@²Ä(g®®)Ϋ«ΒΡΫ«ΤΫΖ÷ΨÄ…œ��ΓΘ
ΆΊ’ΙΘΚ»ΐΫ«–Έ»ΐ²Ä(g®®)Ϋ«ΒΡΫ«ΤΫΖ÷ΨÄΒΡΫΜϋc(di®Θn)ΒΫ»ΐ½lΏÖΒΡΨύκxœύΒ»����ΓΘ
Ϋ«ΤΫΖ÷ΨÄΆ®≥Θ”Ο”Ύ«σϋc(di®Θn)ΒΫ÷±ΨÄΨύκxΓΔ»ΐΫ«–ΈΟφΖeΫ«Ε»�����ΓΘ
ΆΊ’Ι»ΐ²Ä(g®®)Η≈ΡνΘΚ
÷Ί–ΡΘΚ
»ΐΫ«–Έ÷–ΨÄΒΡΫΜϋc(di®Θn)���Θ§÷Ί–ΡΖ÷÷–ΨÄ…œœ¬±»ûι2:1����ΓΘ
É»(n®®i)–ΡΘΚ
»ΐΫ«–ΈΫ«ΤΫΖ÷ΨÄΒΡΫΜϋc(di®Θn)�����Θ§É»(n®®i)–ΡΒΫ»ΐΏÖΒΡΨύκxœύΒ»ΓΘ
Άβ–ΡΘΚ
»ΐΫ«–Έ¥Ι÷±ΤΫΖ÷ΨÄΒΡΫΜϋc(di®Θn)����Θ§Άβ–ΡΒΫ»ΐ²Ä(g®®)μîϋc(di®Θn)ΒΡΨύκxœύΒ»ΓΘ
Ϋ«ΤΫΖ÷ΨÄ≥Θ“äΒΡΥΡΖNίo÷ζΨÄΉωΖ®ΘΚ
ΔΌ»γœ¬àD����Θ§”…Ϋ«ΒΡΤΫΖ÷ΨÄ…œΒΡ“Μϋc(di®Θn)œρΫ«ΒΡ“ΜΏÖΜρÉ…ΏÖΉς¥ΙΨÄΘ§Ω…“‘”ΟΫ«ΒΡΤΫΖ÷ΨÄ–‘Ό|(zh®§)Ε®άμΫβν};
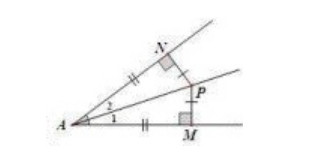
ΔΎ »γœ¬àD�����Θ§“‘Ϋ«ΒΡΤΫΖ÷ΨÄûιίS����Θ§¨ΔàD–ΈΖ≠’έΘ§‘ΎΫ«ΒΡΤΫΖ÷ΨÄÉ…²»(c®®)‰΄(g®Αu)‘λ»ΪΒ»»ΐΫ«–Έ���Θ§ Ι“―÷Σ≈cΫY(ji®Π)’™Αl(f®Γ)…ζξP(gu®Γn)œΒ≥ω§F(xi®Λn)–¬ΒΡ½lΦΰ;

Δέ »γœ¬àD�����Θ§°î(d®Γng)ν}‘O(sh®®)”–Ϋ«ΤΫΖ÷ΨÄΦΑ≈cΫ«ΤΫΖ÷ΨÄ¥Ι÷±ΒΡΨÄΕΈΘ§Ω…―”ιL(zh®Θng)Ώ@½lΨÄΕΈ≈cΫ«ΒΡΝμ“ΜΏÖœύΫΜ����Θ§‰΄(g®Αu)≥…Β»―ϋ»ΐΫ«–Έ��Θ§ άϊ”ΟΒ»―ϋ»ΐΫ«–ΈΒΡ“»ΐΨÄΚœ“Μ” –‘Ό|(zh®§)ΉCν};
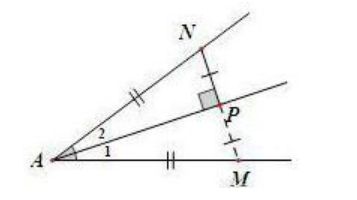
Δή»γœ¬àD���Θ§Ώ^(gu®Α)Ϋ«ΒΡ“ΜΏÖ…œΒΡϋc(di®Θn)Θ§ΉςΝμ“ΜΏÖΒΡΤΫ––ΨÄ����Θ§‰΄(g®Αu)≥…Β»―ϋ»ΐΫ«–Έ——“Ϋ«ΤΫΖ÷ΨÄ+ΤΫ––Θ§±Ί≥ωΒ»―ϋ ”
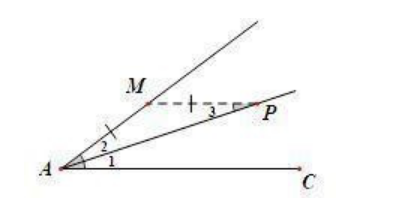
¥Ι÷±ΤΫΖ÷ΨÄ
–‘Ό|(zh®§)Ε®άμΘΚ
ΨÄΕΈ¥Ι÷±ΤΫΖ÷ΨÄ…œΒΡϋc(di®Θn)ΒΫΨÄΕΈÉ…²Ä(g®®)ΕΥϋc(di®Θn)ΒΡΨύκxœύΒ»����ΓΘ
»γΚΈ≈–Ε®ΘΚ
ΒΫΨÄΕΈÉ…²Ä(g®®)ΕΥϋc(di®Θn)ΨύκxœύΒ»ΒΡϋc(di®Θn)‘ΎΏ@½lΨÄΕΈΒΡ¥Ι÷±ΤΫΖ÷ΨÄ…œΓΘ
ΆΊ’ΙΘΚ
»ΐΫ«–Έ»ΐ½lΏÖΒΡ¥Ι÷±ΤΫΖ÷ΨÄΒΡΫΜϋc(di®Θn)ΒΫ»ΐ²Ä(g®®)μîϋc(di®Θn)ΒΡΨύκxœύΒ»����ΓΘ
œύξP(gu®Γn)ΖΫΖ®Ω²ΫY(ji®Π)ΘΚ
≥ω§F(xi®Λn)“Μϋc(di®Θn)ΒΫÉ…ϋc(di®Θn)ΨύκxœύΒ»ΒΡν}–ΆΘ§“ΜΑψ“Σ”ΟΒΫ¥Ι÷±ΤΫΖ÷ΨÄ;
ν}÷–Ω¥ΒΫΨÄΕΈ¥Ι÷±ΤΫΖ÷ΨÄ�����Θ§“ΣœκΒΫ¥Ι÷±ΤΫΖ÷ΨÄ¥Ι÷±«“ΤΫΖ÷ΨÄΕΈ�����Θ§¥Ι÷±ΤΫΖ÷ΨÄ…œϋc(di®Θn)ΒΫΨÄΕΈÉ…ΕΥϋc(di®Θn)ΨύκxœύΒ»Θ§œύΒ»ΏÖΥυ¨Π(du®§)ëΣ(y®©ng)Ϋ«œύΒ»;
Ζ≠’έν}–Ά÷–≥Θ”ΟΒΫ¥Ι÷±ΤΫΖ÷ΨÄ�����ΓΔΙ¥Ι…Ε®άμ����ΓΘ
Β»―ϋ»ΐΫ«–Έ
–‘Ό|(zh®§)Ε®άμΘΚ
Β»―ϋ»ΐΫ«–ΈΒΡÉ…²Ä(g®®)ΒΉΫ«œύΒ»(Β»ΏÖ¨Π(du®§)Β»Ϋ«)
Β»―ϋ»ΐΫ«–ΈΒΡμîΫ«ΤΫΖ÷ΨÄΓΔΒΉΏÖ…œΒΡ÷–ΨÄ�����ΓΔΒΉΏÖ…œΒΡΗΏΨÄΜΞœύ÷ΊΚœ(»ΐΨÄΚœ“Μ)
≈–îύΘΚ“Μ²Ä(g®®)»ΐΫ«–ΈΒΡÉ…²Ä(g®®)œύΒ»ΒΡΫ«Υυ¨Π(du®§)ΒΡΏÖ“≤œύΒ»(Β»Ϋ«¨Π(du®§)Β»ΏÖ)
Β»ΏÖ»ΐΫ«–Έ
–‘Ό|(zh®§)Ε®άμΘΚ
Β»ΏÖ»ΐΫ«–ΈΒΡ»ΐ½lΏÖΕΦœύΒ»;
Β»ΏÖ»ΐΫ«–ΈΒΡ»ΐ²Ä(g®®)É»(n®®i)Ϋ«ΕΦœύΒ»�����Θ§ΕΦΒ»”Ύ60Ε»����ΓΘΒ»ΏÖ»ΐΫ«–ΈΒΡΟΩ“Μ½lΏÖΕΦΡήΏ\(y®¥n)”Ο»ΐΨÄΚœ“ΜΏ@“Μ–‘Ό|(zh®§)ΓΘ
≈–îύΕ®άμΘΚ
»ΐ½lΏÖΕΦœύΒ»ΒΡ»ΐΫ«–Έ «Β»ΏÖ»ΐΫ«–Έ;
»ΐ²Ä(g®®)Ϋ«ΕΦœύΒ»ΒΡ»ΐΫ«–Έ «Β»ΏÖ»ΐΫ«–Έ;
”–É…²Ä(g®®)Ϋ« « 60°ΒΡ»ΐΫ«–Έ «Β»ΏÖ»ΐΫ«–Έ;
”–“Μ²Ä(g®®)Ϋ« « 60°ΒΡΒ»―ϋ»ΐΫ«–Έ «Β»ΏÖ»ΐΫ«–Έ����ΓΘ
ΖΫΖ®Ω²ΫY(ji®Π)ΘΚ≥ω§F(xi®Λn)Β»―ϋ»ΐΫ«–ΈΆ®≥Θ“ΣΖ÷νê”ë’™Θ§‘ΎΏx™ών}ΚΆΧνΩ’ν}÷–��Θ§«–Έπ“ρ?y®Λn)ι¦](m®Πi)”–Ζ÷νê”ë’™Εχ¨ß(d®Θo)÷¬Ηψεe(cu®Α)¥πΑΗ��ΓΘ
÷±Ϋ«»ΐΫ«–ΈΚΆΙ¥Ι…Ε®άμ
”–“Μ²Ä(g®®)Ϋ« «÷±Ϋ«ΒΡ»ΐΫ«–Έ «÷±Ϋ«»ΐΫ«–Έ���Θ§‘Ύ÷±Ϋ«»ΐΫ«–Έ÷–����Θ§–±ΏÖ÷–ΨÄΒ»”Ύ–±ΏÖΒΡ“ΜΑκ;
30Ε»Υυ¨Π(du®§)ΒΡ÷±Ϋ«ΏÖΒ»”Ύ–±ΏÖΒΡ“ΜΑκ;÷±Ϋ«»ΐΫ«–Έ≥Θ”ΟΟφΖeΖ®«σ–±ΏÖ…œΒΡΗΏ��ΓΘ
Ι¥Ι…Ε®άμΘΚ
÷±Ϋ«»ΐΫ«–ΈÉ…÷±Ϋ«ΏÖ a����Θ§b ΒΡΤΫΖΫΚΆΒ»”Ύ–±ΏÖ c ΒΡΤΫΖΫΘ§Φ¥ a2+b2=c2��ΓΘ
Ι¥Ι…îΒ(sh®¥)“ΜΕ® «’ΐ’ϊîΒ(sh®¥)���Θ§≥Θ“äΙ¥Ι…îΒ(sh®¥)ΘΚ
3,4,5;
5,12,13;
6,8,10,;
7,24,25;
8,15,17;
9,12,15����ΓΘ
ΖΫΖ®Ω²ΫY(ji®Π)ΘΚ
°î(d®Γng)≤ΜΟς¥_÷±Ϋ«»ΐΫ«–ΈΒΡ–±ΏÖιL(zh®Θng)��Θ§ëΣ(y®©ng)Α―“―÷ΣΉνιL(zh®Θng)ΏÖΖ÷ûι÷±Ϋ«ΏÖΚΆ–±ΏÖÉ…ΖN«ι¦r”ë’™��ΓΘ
üo(w®≤)άμîΒ(sh®¥)‘ΎîΒ(sh®¥)ίS…œΒΡ±μ ΨΚΆΨÄΕΈιL(zh®Θng)±μ ΨΆ®≥Θ”ΟΒΫΙ¥Ι…Ε®άμΓΘ
Ζ≠’έν}–Ά≥Θ”ΟΙ¥Ι…Ε®άμ(ΩΎ‘EΘΚΖ≠’έ«σΏÖ’“÷±Ϋ«����Θ§Ι¥Ι…Ε®άμ‘O(sh®®)Έ¥÷ΣΝΩ)
»γΙϊ»ΐΫ«–ΈΒΡ»ΐΏÖιL(zh®Θng) aΘ§b����Θ§c ”–ξP(gu®Γn)œΒ a2+b2=c2Θ§Ρ«Ο¥Ώ@²Ä(g®®)»ΐΫ«–Έ «÷±Ϋ«»ΐΫ«–Έ���ΓΘΙ¥Ι…Ε®άμΒΡΡφΕ®άμ�����Θ§≥Θ”Ο”Ύ≈–îύ»ΐΫ«–ΈΒΡ–Έ†ν��Θ§œ»¥_Ε®Ήν¥σΏÖ(Ω…“‘‘O(sh®®)ûιc)

Ψéί΄ΆΤΥ]ΘΚ
2024Ρξ÷–ΩΦΗςΩΤΡΩ÷Ίϋc(di®Θn)÷ΣΉR(sh®Σ)ÖRΩ²
ΓΓΓΓΉν–¬÷–ΩΦΌY”ç�����ΓΔ÷–ΩΦ’ΰ≤Ώ�����ΓΔΩΦ«Α€ (zh®≥n)²δ��ΓΔ÷–ΩΦνA(y®¥)€y(c®®)����ΓΔ䦻ΓΖ÷?j®Ϊn)?sh®¥)ΨÄΒ»
ΓΓΓΓ÷–ΩΦïr(sh®Σ)ιgΨÄΒΡ»Ϊ≤Ω÷Ί“ΣΙù(ji®Π)ϋc(di®Θn)
ΓΓΓΓ±M‘Ύ"÷–ΩΦΨW(w®Θng)"ΈΔ–≈ΙΪ±äΧ•(h®Λo)

ΓΓΓΓ ög”≠ Ι”Ο ÷ôC(j®©)��ΓΔΤΫΑεΒ»“Τ³”(d®Αng)‘O(sh®®)²δ‘LÜ•(w®®n)÷–ΩΦΨW(w®Θng)�����Θ§2024÷–ΩΦ“Μ¬Ζ≈ψΑιΆ§––����ΘΓ>>ϋc(di®Θn)™τ≤ιΩ¥















