ϋc(di®Θn)ΒΡΉχ‰Υ(bi®Γo)ΧΊ’ς
01
ΒΎ“ΜœσœόÉ»(n®®i)ΒΡϋc(di®Θn)ôMΉχ‰Υ(bi®Γo)ûι’ΐΘ§ΩvΉχ‰Υ(bi®Γo)ûι’ΐΘ§Φ¥(+��Θ§+);ΒΎΕΰœσœόÉ»(n®®i)ΒΡϋc(di®Θn)ôMΉχ‰Υ(bi®Γo)ûιΊ™(f®¥)Θ§ΩvΉχ‰Υ(bi®Γo)Wie’ΐ�����Θ§Φ¥(—����Θ§+);ΒΎ»ΐœσœόÉ»(n®®i)ΒΡϋc(di®Θn)ôMΉχ‰Υ(bi®Γo)ûιΊ™(f®¥)�����Θ§ΩvΉχ‰Υ(bi®Γo)ûιΊ™(f®¥)�����Θ§Φ¥(—���Θ§—);ΒΎΥΡœσœόÉ»(n®®i)ΒΡϋc(di®Θn)ôMΉχ‰Υ(bi®Γo)ûι’ΐ�����Θ§ΩvΉχ‰Υ(bi®Γo)ûιΊ™(f®¥)��Θ§Φ¥(+���Θ§—)�ΓΘ
άΐν}1ΘΚ»τϋc(di®Θn)A(a+1��Θ§b-2)‘ΎΒΎΕΰœσœό���Θ§³tϋc(di®Θn)B(-a��Θ§1-b)‘ΎΒΎ( )œσœό�����ΓΘ
ΫβΘΚΓΏϋc(di®Θn)A(a+1���Θ§b-2)‘ΎΒΎΕΰœσœόΘ§
∴a+1<0�����Θ§b-2>0Θ§
ΫβΒΟΘΚa<-1�Θ§b>2Θ§
³t-a>1�Θ§1-b<-1Θ§
Ι ϋc(di®Θn)B(-a��Θ§1-b)‘ΎΒΎΥΡœσœό
Ϋβ¥Υνê(l®®i)Ü•(w®®n)ν}ΒΡ“ΜΑψΖΫΖ® «Ηυ™ΰ(j®¥)ϋc(di®Θn)‘ΎΉχ‰Υ(bi®Γo)œΒΒΡΖϊΧ•(h®Λo)ΧΊ’ς���Θ§Ϋ®ΝΔ≤ΜΒ» Ϋ(ΫM)ΜρΖΫ≥Χ(ΫM)���Θ§Α―ϋc(di®Θn)ΒΡÜ•(w®®n)ν}όD(zhu®Θn)Μ·ûι≤ΜΒ» Ϋ(ΫM)ΜρΖΫ≥Χ(ΫM)¹μ(l®Δi)Ϋβ¦QΓΘ
ϋc(di®Θn)ΒΡΤΫ“Τ≈c¨Π(du®§)ΖQ(ch®Ξng)
02
Ήσ”“ΤΫ“Τ�����Θ§ΗΡΉÉΒΡûιϋc(di®Θn)ΒΡôMΉχ‰Υ(bi®Γo)���ΓΘϋc(di®Θn)(xΘ§y)œρΉσΤΫ“Τa²Ä(g®®)ÜΈΈΜ����Θ§ΒΟΒΫΒΡϋc(di®Θn)Ήχ‰Υ(bi®Γo)ûι(x-a����Θ§b)�����Θ§œρ”“ΤΫ“Τb²Ä(g®®)ÜΈΈΜ����Θ§ΒΟΒΫΒΡϋc(di®Θn)Ήχ‰Υ(bi®Γo)ûι(x+bΘ§y)�ΓΘ…œœ¬ΤΫ“ΤΘ§ΗΡΉÉΒΡûιϋc(di®Θn)ΒΡΩvΉχ‰Υ(bi®Γo)�ΓΘϋc(di®Θn)(xΘ§y)œρ…œΤΫ“Τa²Ä(g®®)ÜΈΈΜ���Θ§ΒΟΒΫΒΡϋc(di®Θn)Ήχ‰Υ(bi®Γo)ûι(x����Θ§y+a)�����Θ§œρœ¬ΤΫ“Τb²Ä(g®®)ÜΈΈΜΘ§ΒΟΒΫΒΡϋc(di®Θn)Ήχ‰Υ(bi®Γo)ûι(x����Θ§y-b)ΓΘ
άΐν}2ΘΚ“―÷ΣΨÄΕΈCD «”…ΨÄΕΈABΤΫ“ΤΒΟΒΫΒΡ���Θ§ϋc(di®Θn)A(-1����Θ§2)ΒΡ¨Π(du®§)ëΣ(y®©ng)ϋc(di®Θn)ûιC(3�Θ§1)Θ§³tϋc(di®Θn)B(-2�Θ§-2)ΒΡ¨Π(du®§)ëΣ(y®©ng)ϋc(di®Θn)DΒΡΉχ‰Υ(bi®Γo)ûι( )
ΫβΘΚ”…ϋc(di®Θn)A(-1Θ§2)ΒΡ¨Π(du®§)ëΣ(y®©ng)ϋc(di®Θn)ûιC(3����Θ§1)Θ§÷ΣΨÄΕΈABœρ”“ΤΫ“Τ4²Ä(g®®)ÜΈΈΜ���ΓΔœρœ¬ΤΫ“Τ1²Ä(g®®)ÜΈΈΜΦ¥Ω…ΒΟΒΫCDΘ§
∴ϋc(di®Θn)B(-2����Θ§-2)ΒΡ¨Π(du®§)ëΣ(y®©ng)ϋc(di®Θn)DΒΡΉχ‰Υ(bi®Γo)ûι(-2+4Θ§-2-1)Θ§Φ¥(2���Θ§-3)�����Θ§
ξP(gu®Γn)”ΎxίS¨Π(du®§)ΖQ(ch®Ξng)ΒΡϋc(di®Θn)��Θ§ôMΉχ‰Υ(bi®Γo)œύΆ§��Θ§ΩvΉχ‰Υ(bi®Γo)ΜΞûιœύΖ¥îΒ(sh®¥);ξP(gu®Γn)”ΎyίS¨Π(du®§)ΖQ(ch®Ξng)ΒΡϋc(di®Θn)�Θ§ΩvΉχ‰Υ(bi®Γo)œύΆ§���Θ§ôMΉχ‰Υ(bi®Γo)ΜΞûιœύΖ¥îΒ(sh®¥);ξP(gu®Γn)”Ύ‘≠ϋc(di®Θn)¨Π(du®§)ΖQ(ch®Ξng)ΒΡϋc(di®Θn)��Θ§ôM�����ΓΔΩvΉχ‰Υ(bi®Γo)ΕΦΜΞûιœύΖ¥îΒ(sh®¥)���ΓΘ
άΐν}3ΘΚ¨Δ»ΐΫ«–Έ»ΐ²Ä(g®®)μîϋc(di®Θn)ΒΡôMΉχ‰Υ(bi®Γo)ΕΦ≥Υ“‘-1Θ§ΩvΉχ‰Υ(bi®Γo)≤ΜΉÉ�Θ§³tΥυΒΟ»ΐΫ«–Έ≈c‘≠»ΐΫ«–ΈΒΡξP(gu®Γn)œΒ «
ΫβΘΚ”…ν}“β�����Θ§ôMΉχ‰Υ(bi®Γo)ΜΞûιœύΖ¥îΒ(sh®¥)���Θ§ΩvΉχ‰Υ(bi®Γo)≤ΜΉÉΘ§Ρ«Ο¥É…²Ä(g®®)àD–ΈξP(gu®Γn)”ΎxίS¨Π(du®§)ΖQ(ch®Ξng)���ΓΘ
ΉÉ ΫΘΚ¨Δ»ΐΫ«–Έ»ΐ²Ä(g®®)μîϋc(di®Θn)ΒΡôMΉχ‰Υ(bi®Γo)ΕΦ€p2����Θ§ΩvΉχ‰Υ(bi®Γo)≤ΜΉÉ��Θ§³tΥυΒΟ»ΐΫ«–Έ≈c‘≠»ΐΫ«–ΈΒΡξP(gu®Γn)œΒ «
ΫβΘΚΓΏ¨Δ»ΐΫ«–Έ»ΐ²Ä(g®®)μîϋc(di®Θn)ΒΡôMΉχ‰Υ(bi®Γo)ΕΦ€p2���Θ§ΩvΉχ‰Υ(bi®Γo)≤ΜΉÉ��Θ§
∴ΥυΒΟ»ΐΫ«–Έ≈c‘≠»ΐΫ«–ΈΒΡξP(gu®Γn)œΒ «ΘΚ¨Δ‘≠àDœρΉσΤΫ“ΤÉ…²Ä(g®®)ÜΈΈΜ.
‘ΎΤΫΟφ÷±Ϋ«Ήχ‰Υ(bi®Γo)œΒÉ»(n®®i)�Θ§Α―“Μ²Ä(g®®)àD–ΈΗς²Ä(g®®)ϋc(di®Θn)ΒΡôMΉχ‰Υ(bi®Γo)ΕΦΦ”…œ(Μρ€p»Ξ)“Μ²Ä(g®®)’ϊîΒ(sh®¥)a�Θ§œύëΣ(y®©ng)ΒΡ–¬àD–ΈΨΆ «Α―‘≠àD–Έœρ”“(ΜρœρΉσ)ΤΫ“Τa²Ä(g®®)ÜΈΈΜιL(zh®Θng)Ε»;»γΙϊΑ―ΥϋΗς²Ä(g®®)ϋc(di®Θn)ΒΡΩvΉχ‰Υ(bi®Γo)ΕΦΦ”(Μρ€p»Ξ)“Μ²Ä(g®®)’ϊîΒ(sh®¥)aΘ§œύëΣ(y®©ng)ΒΡ–¬àD–ΈΨΆ «Α―‘≠àD–Έœρ…œ(Μρœρœ¬)ΤΫ“Τa²Ä(g®®)ÜΈΈΜιL(zh®Θng)Ε».(Φ¥ΘΚôMΉχ‰Υ(bi®Γo)�Θ§”““ΤΦ”Θ§Ήσ“Τ€p;ΩvΉχ‰Υ(bi®Γo)��Θ§…œ“ΤΦ”����Θ§œ¬“Τ€p)
ΈΜ÷ΟΒΡ¥_Ε®
03
”…“―÷Σ½lΦΰΫ®ΝΔΚœΏmΒΡ÷±Ϋ«Ήχ‰Υ(bi®Γo)œΒΒΡξP(gu®Γn)φI «ΘΚ(1)“Σ’ΐ¥_¥_Ε®Ήχ‰Υ(bi®Γo)‘≠ϋc(di®Θn)ΒΡΈΜ÷Ο;(2)“Σ€ (zh®≥n)¥_¥_Ε®ÜΈΈΜιL(zh®Θng)Ε»ΓΘ
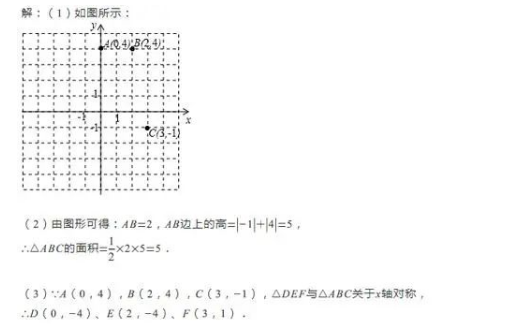
άΐν}4ΘΚΤΫΟφ÷±Ϋ«Ήχ‰Υ(bi®Γo)œΒ÷–����Θ§ΓςABCΒΡ»ΐ²Ä(g®®)μîϋc(di®Θn)Ήχ‰Υ(bi®Γo)Ζ÷³eûιA(0Θ§4)B(2�����Θ§4)C(3���Θ§-1).
(1)‘΅‘ΎΤΫΟφ÷±Ϋ«Ήχ‰Υ(bi®Γo)œΒ÷–�����Θ§‰Υ(bi®Γo)≥ωA�ΓΔB�ΓΔC»ΐϋc(di®Θn);
(2)«σΓςABCΒΡΟφΖe.
(3)»τΓςDEF≈cΓςABCξP(gu®Γn)”ΎxίS¨Π(du®§)ΖQ(ch®Ξng)Θ§¨ë(xi®ß)≥ωD��ΓΔE�����ΓΔFΒΡΉχ‰Υ(bi®Γo).
Ζ÷ΈωΘΚ(1)Ηυ™ΰ(j®¥)»ΐϋc(di®Θn)ΒΡΉχ‰Υ(bi®Γo)Θ§‘Ύ÷±Ϋ«Ήχ‰Υ(bi®Γo)œΒ÷–Ζ÷³e‰Υ(bi®Γo)≥ωΈΜ÷ΟΦ¥Ω….(2)“‘ABûιΒΉ��Θ§³tϋc(di®Θn)CΒΫABΒΡΨύκxΦ¥ «ΒΉΏÖABΒΡΗΏ����Θ§ΫY(ji®Π)ΚœΉχ‰Υ(bi®Γo)œΒΩ…ΒΟ≥ωΗΏûιϋc(di®Θn)CΒΡΩvΉχ‰Υ(bi®Γo)ΒΡΫ^¨Π(du®§)÷ΒΦ”…œϋc(di®Θn)BΒΡΩvΉχ‰Υ(bi®Γo)ΒΡΫ^¨Π(du®§)÷ΒΘ§èΡΕχΗυ™ΰ(j®¥)»ΐΫ«–ΈΒΡΟφΖeΙΪ Ϋ”΄(j®§)ΥψΦ¥Ω….(3)ξP(gu®Γn)”ΎxίS¨Π(du®§)ΖQ(ch®Ξng)ΒΡϋc(di®Θn)ΒΡΉχ‰Υ(bi®Γo)�����Θ§ôMΉχ‰Υ(bi®Γo)≤ΜΉÉ�Θ§ΩvΉχ‰Υ(bi®Γo)ΜΞûιœύΖ¥îΒ(sh®¥)Θ§èΡΕχΩ…ΒΟ≥ωD��ΓΔE�ΓΔFΒΡΉχ‰Υ(bi®Γo).
±Ψν}ΩΦ≤ιΝΥΉχ‰Υ(bi®Γo)≈càD–Έ–‘Ό|(zh®§)Θ§ίS¨Π(du®§)ΖQ(ch®Ξng)ΉςàD�����Θ§»ΐΫ«–ΈΒΡΟφΖe�Θ§Ϋβ¥π±Ψν}ΒΡξP(gu®Γn)φI «’ΐ¥_ΒΡ’“≥ω»ΐϋc(di®Θn)ΒΡΈΜ÷ΟΘ§ΝμΆβ“Σ’ΤΈ’ξP(gu®Γn)”ΎxίS¨Π(du®§)ΖQ(ch®Ξng)ΒΡϋc(di®Θn)ΒΡΉχ‰Υ(bi®Γo)ΒΡΧΊϋc(di®Θn)�ΓΘ
“é(gu®©)¬…ΧΫΨΩ
04
“‘―≠≠h(hu®Δn)ûιΧΊ’ςΒΡ“é(gu®©)¬…ΧΫΥς–ΆÜ•(w®®n)ν}�����Θ§Ϋβ¦Q¥Υνê(l®®i)Ü•(w®®n)ν}ëΣ(y®©ng)œ»”^≤λàD–ΈΒΡΉÉΜ·ΎÖ³ί(sh®§)Θ§»ΜΚσ¨Π(du®§)ΒΎ“Μ²Ä(g®®)àD–ΈΏM(j®§n)––Ζ÷Έω�Θ§Ώ\(y®¥n)”ΟèΡΧΊ βΒΫ“ΜΑψΒΡΧΫΥςΖΫ ΫΘ§»γΙϊ“‘m¥Έûι“Μ²Ä(g®®)―≠≠h(hu®Δn)��ȧѫϥ¾n¥ΈΒΡ«ι–Έ≈cn÷mΒΡ”ύîΒ(sh®¥) «œύΆ§ΒΡ�����Θ§’ϊ≥ΐïr(sh®Σ)≈cΉνΚσ“Μ¥Έ«ι–ΈœύΆ§�����ΓΘ
άΐν}5ΘΚ»γàD�����Θ§÷±Ϋ«Ήχ‰Υ(bi®Γo)ΤΫΟφxOyÉ»(n®®i)�����Θ§³”(d®Αng)ϋc(di®Θn)PΑ¥àD÷–Φΐν^Υυ ΨΖΫœρ“ά¥ΈΏ\(y®¥n)³”(d®Αng)��Θ§ΒΎ1¥ΈèΡϋc(di®Θn)(-1Θ§0)Ώ\(y®¥n)³”(d®Αng)ΒΫϋc(di®Θn)(0����Θ§1)Θ§ΒΎ2¥ΈΏ\(y®¥n)³”(d®Αng)ΒΫϋc(di®Θn)(1��Θ§0)���Θ§ΒΎ3¥ΈΏ\(y®¥n)³”(d®Αng)ΒΫϋc(di®Θn)(2�Θ§-2)�Θ§…Α¥Ώ@‰”ΒΡΏ\(y®¥n)³”(d®Αng)“é(gu®©)¬…Θ§³”(d®Αng)ϋc(di®Θn)PΒΎ2020¥ΈΏ\(y®¥n)³”(d®Αng)ΒΫϋc(di®Θn)( )
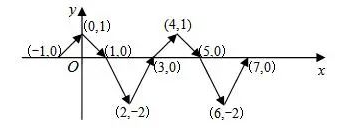
Ζ÷ΈωΘΚ”^≤λàD–ΈΩ…÷Σ���Θ§ΟΩ4¥ΈΏ\(y®¥n)³”(d®Αng)ûι“Μ²Ä(g®®)―≠≠h(hu®Δn)ΫM―≠≠h(hu®Δn)����Θ§≤Δ«“ΟΩ“Μ²Ä(g®®)―≠≠h(hu®Δn)ΫMœρ”“Ώ\(y®¥n)³”(d®Αng)4²Ä(g®®)ÜΈΈΜ��Θ§”Ο2020≥ΐ“‘4��Θ§»ΜΚσΗυ™ΰ(j®¥)…ΧΚΆ”ύîΒ(sh®¥)ΒΡ«ι¦r¥_Ε®Ώ\(y®¥n)³”(d®Αng)Κσϋc(di®Θn)ΒΡΉχ‰Υ(bi®Γo)Φ¥Ω….
ΫβΘΚΓΏ2020÷4=505��Θ§
∴³”(d®Αng)ϋc(di®Θn)PΒΎ2020¥ΈΏ\(y®¥n)³”(d®Αng)ûιΒΎ505²Ä(g®®)―≠≠h(hu®Δn)ΫMΒΡΒΎ4¥ΈΏ\(y®¥n)³”(d®Αng)Θ§ôMΉχ‰Υ(bi®Γo)505×4-1=2019�Θ§ΩvΉχ‰Υ(bi®Γo)ûι0Θ§
∴ϋc(di®Θn)P¥Υïr(sh®Σ)Ήχ‰Υ(bi®Γo)ûι(2019��Θ§0).
ΤΫΟφ÷±Ϋ«Ήχ‰Υ(bi®Γo)œΒœ¬ΒΡ“é(gu®©)¬…ΧΫΨΩν}����Θ§Ϋβ¥πïr(sh®Σ)ΉΔ“βΧΫΨΩ³”(d®Αng)ϋc(di®Θn)ΒΡΏ\(y®¥n)³”(d®Αng)“é(gu®©)¬…Θ§”÷“ΣΉΔ“β³”(d®Αng)ϋc(di®Θn)ΒΡΉχ‰Υ(bi®Γo)ΒΡœσœόΖϊΧ•(h®Λo)��ΓΘ
Ψéί΄ΆΤΥ]ΘΚ
2023Ρξ÷–ΩΦΗςΩΤΡΩ÷Ίϋc(di®Θn)÷ΣΉR(sh®Σ)ÖRΩ²
ΓΓΓΓΉν–¬÷–ΩΦΌY”ç�����ΓΔ÷–ΩΦ’ΰ≤Ώ���ΓΔΩΦ«Α€ (zh®≥n)²δΓΔ÷–ΩΦνA(y®¥)€y(c®®)�����ΓΔ䦻ΓΖ÷?j®Ϊn)?sh®¥)ΨÄΒ»
ΓΓΓΓ÷–ΩΦïr(sh®Σ)ιgΨÄΒΡ»Ϊ≤Ω÷Ί“ΣΙù(ji®Π)ϋc(di®Θn)
ΓΓΓΓ±M‘Ύ"÷–ΩΦΨW(w®Θng)"ΈΔ–≈ΙΪ±äΧ•(h®Λo)

ΓΓΓΓ ög”≠ Ι”Ο ÷ôC(j®©)��ΓΔΤΫΑεΒ»“Τ³”(d®Αng)‘O(sh®®)²δ‘LÜ•(w®®n)÷–ΩΦΨW(w®Θng)���Θ§2023÷–ΩΦ“Μ¬Ζ≈ψΑιΆ§––����ΘΓ>>ϋc(di®Θn)™τ≤ιΩ¥












