Ζ¥±»άΐΚ·îΒ(sh®¥)‘Ύ≥θ÷–îΒ(sh®¥)¨WΒΡΚ·îΒ(sh®¥)¨WΝï÷–�����Θ§’Φ™ΰ(j®¥)÷χί^ûι÷Ί“ΣΒΡΈΜ÷Ο�ΓΘœ¬ΟφΈ“²É¹μ αάμ“Μœ¬”–ξPΖ¥±»άΐΚ·îΒ(sh®¥)ΒΡ÷ΣΉR:
Ζ¥±»άΐΚ·îΒ(sh®¥)ΒΡΜυ±ΨÉ»(n®®i)»ί
Ε®Νx:
»γΙϊÉ…²ÄΉÉΝΩxΘ§y÷°ιgΒΡ¨ΠëΣξPœΒΩ…“‘±μ Ψ≥…y=k/x(kûι≥ΘîΒ(sh®¥)�����Θ§k≠0)ΒΡ–Έ Ϋ���Θ§Ρ«Ο¥ΖQy «xΒΡΖ¥±»άΐΚ·îΒ(sh®¥)���ΓΘΚ·îΒ(sh®¥)±μΏ_ ΫûιΘΚ
Γτ y=k/x
Γτ y=kxΓΞ1
Γτ xy=k
ΉΔ“βΘΚΖ¥±»άΐΚ·îΒ(sh®¥)≥…ΝΔΒΡ½lΦΰ «ΘΚkûι≥ΘîΒ(sh®¥)«“k≠0ΓΘ‘™½lΦΰΆ§ïr≥…ΝΔ���Θ§Ά§¨W‘ΎΫβν}Ώ^≥Χ÷–ΆυΆυ»ί“ΉΚω“ïΤδ≥…ΝΔ½lΦΰ�Θ§èΡΕχ‘Ύ»Γ÷ΒΖΕ΅ζΒΡ¥_Ε®÷–“Ή≥ωεeΓΘ
Κ·îΒ(sh®¥)ΒΡ‘ω€p–‘:
°îk>0ïr�Θ§àDœσΖ÷³eΈΜ”ΎΒΎ“Μ����ΓΔ»ΐœσœόΘ§Ά§“Μ²ÄœσœόÉ»(n®®i)��Θ§yκSxΒΡ‘ω¥σΕχ€p–Γ;
°îk<0ïr�����Θ§àDœσΖ÷³eΈΜ”ΎΕΰ�����ΓΔΥΡœσœό���Θ§Ά§“Μ²ÄœσœόÉ»(n®®i),yκSxΒΡ‘ω¥σΕχ‘ω¥σ��ΓΘ
–‘Ό|(zh®§)ΘΚ
(1)Ζ¥±»άΐΚ·îΒ(sh®¥)…œ»ΈΚΈ“Μϋc≈cίSΨÄ΅ζ≥«ΒΡ÷±Ϋ«»ΐΫ«–ΈΟφΖeΕΦœύΒ»|k|/2;
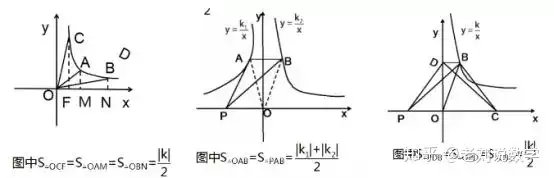
(2)àDœώ…œ»Έ“βÉ…ϋc≈c‘≠ϋc‰΄≥…ΒΡ»ΐΫ«–ΈΒΡΟφΖeΒ»”Ύ÷±Ϋ«Χί–ΈΒΡΟφΖe;
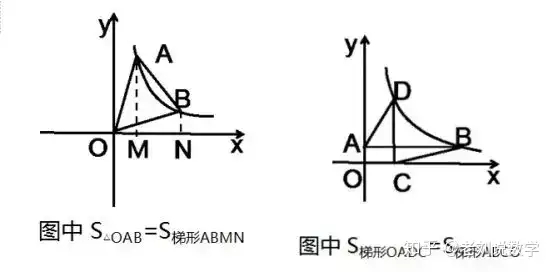
(3)Ζ¥±»άΐΚ·îΒ(sh®¥)≈c“Μ¥ΈΚ·îΒ(sh®¥)œύΫΜïrΘ§¥φ‘ΎΨÄΕΈœύΒ»ΒΡξPœΒΘ§Ήχ‰ΥϋcξP”Ύ‘≠ϋc¨ΠΖQΒΡξPœΒ;
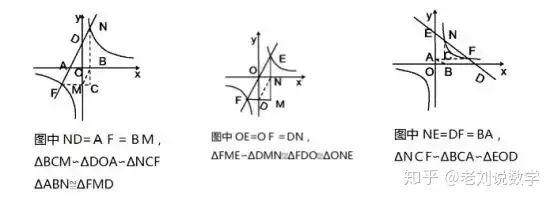
(4)Ζ¥±»άΐ≈c“Μ¥ΈΚ·îΒ(sh®¥)”–ΫΜϋcïr���Θ§Ω…“‘¬™(li®Δn)ΝΔ«σ≥ωΫΜϋcΉχ‰Υ(Εΰ¥Έ¬™(li®Δn)ΝΔΩ…“‘«σ“Μ‘ΣΕΰ¥ΈΖΫ≥Χ���Θ§Ζ¥”≥ΖΫ≥ΧΗυΒΡ²ÄîΒ(sh®¥)Ü•ν})�����ΓΘ
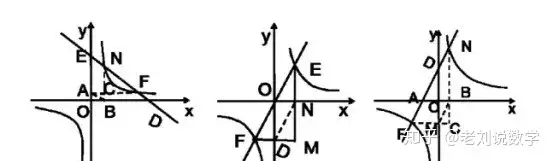
Ζ¥±»άΐΚ·îΒ(sh®¥)≥���ΘΩΦν}–Ά
ΫYΚœΫϋéΉΡξΒΡΩΦ«ιΖ÷Έω���Θ§Ζ¥±»άΐΚ·îΒ(sh®¥)ΆυΆυ≥ω§F(xi®Λn)‘ΎΧνΩ’ν}ΚΆΫβ¥πν}÷–Θ§Τδ≥ων}νê–Ά“ΜΑψ≈c“Μ¥ΈΚ·îΒ(sh®¥)�����ΓΔ»ΐΫ«Κ·îΒ(sh®¥)��ΓΔœύΥΤ�ΓΔ»ΪΒ»��ΓΔàAΒ»œύΫYΚœΘ§≥…ûι¨W…ζΒΡ““Μ¥σ’œΒK”�����Θ§ΒΪ «ΤδÜΈΣö≥ων}ïrΘ§œύ¨ΠΚÜÜΈ��ΓΘ
≈–îύΚ·îΒ(sh®¥)àDœώ
ΔΌ Ω¥œΒîΒ(sh®¥)ΘΚ“Μ¥ΈΚ·îΒ(sh®¥)÷Μ”–“Μ²ÄΈ¥÷ΣîΒ(sh®¥)a;
ΉΔ“βΘΚ»τ“Μ¥ΈΚ·îΒ(sh®¥)ΒΡ“Μ¥Έμ½œΒîΒ(sh®¥)≈cΖ¥±»άΐΚ·îΒ(sh®¥)ΒΡΖ¥±»άΐœΒîΒ(sh®¥)’ΐΊ™œύΆ§�����Θ§÷±ΨÄ≈cκp«ζΒΡÉ…÷ßΕΦ”–ΫΜϋc�����ΓΘ
ΔΎ ’“Ο§ΕήΘΚΆ®≥Θ–η“ΣΏ\”Ο≈≈≥ΐΖ®Θ§≈≈≥ΐεe’`Ώxμ½ΒΟΒΫ’ΐ¥_¥πΑΗ�ΓΘΖ¥±»άΐΚ·îΒ(sh®¥)÷Μ”–“Μ²ÄΈ¥÷ΣîΒ(sh®¥)�Θ§“ρ¥Υ≥ΘèΡΖ¥±»άΐΚ·îΒ(sh®¥)ΒΡàDœσ»κ ÷ΏM––≈–îύ�ΓΘ»γΙϊa>0�����Θ§Ζ¥±»άΐΚ·îΒ(sh®¥)àDœώ‘ΎΒΎ“Μ��ΓΔ»ΐœσœό�Θ§»γΙϊa<0�����Θ§Ζ¥±»άΐΚ·îΒ(sh®¥)àDœσ‘ΎΒΎΕΰ����ΓΔΥΡœσœό�ΓΘ
ΉΔ“βΘΚ°îΖ¥±»άΐΚ·îΒ(sh®¥)≈cΤδΥϊΚ·îΒ(sh®¥)œύΫYΚœ≥ων}ïr����Θ§–η“Σ‘Ό≈–îύΤδΥϊΚ·îΒ(sh®¥)àDœσΫ¦(j®©ng)Ώ^ΒΡœσœόΨΆΩ…¥_Ε®ΤδΚ·îΒ(sh®¥)àDœώΓΘ
«σΫβΈω Ϋ“ΜΑψ–η“Σ«σ≥ωΚ·îΒ(sh®¥)àDœσ…œΒΡϋcΒΡΉχ‰Υ���Θ§Κ·îΒ(sh®¥)ΫβΈω Ϋ…œ”–éΉ²ÄΈ¥÷ΣîΒ(sh®¥)���Θ§ΨΆ“Σ’“?gu®©)Ή²ÄϋcΓΘ
Κ·îΒ(sh®¥)àDœώάL÷Τ≤ΫσEΘΚΝ–±μ---Οηϋc---ΏBΨÄ
(1)Ν–±μ»Γ÷Βïr���Θ§x≠0��Θ§“ρûιx=0Κ·îΒ(sh®¥)üo“βΝx���Θ§ûιΝΥ ΙΟη≥ωΒΡϋcΨΏ”–¥ζ±μ–‘Θ§Ω…“‘“‘“0”ûι÷––Ρ�Θ§œρÉ…ΏÖ¨ΠΖQ Ϋ»Γ÷ΒΘ§Φ¥’ΐ����ΓΔΊ™îΒ(sh®¥)Ης“ΜΑκ�����Θ§«“ΜΞûιœύΖ¥îΒ(sh®¥)Θ§Ώ@‰”“≤±ψ”Ύ«σy÷Β�����ΓΘ
(2)”…”ΎΚ·îΒ(sh®¥)àDœσΒΡΧΊ’ςΏÄ≤Μ«ε≥ΰ����Θ§±MΝΩΕύ»Γ“Μ–©îΒ(sh®¥)÷Β���Θ§ΕύΟη“Μ–©ϋc��Θ§èΡΕχ±ψ”ΎΏBΨÄ���Θ§ Ι°΄≥ωΒΡàDœσΗϋΨΪ¥_�����ΓΘ
(3)ΏBΨÄïr“Σ”ΟΤΫΜ§ΒΡ«ζΨÄΑ¥’’Ή‘ΉÉΝΩèΡ–ΓΒΫ¥σΒΡμ‰–ρΏBΫ”�����Θ§«–Φ…°΄≥…’έΨÄ�ΓΘ
“ρûιΫβΈω Ϋ÷–�Θ§x≤ΜΡήûι0�����Θ§Υυ“‘y“≤≤ΜΡήûι0Θ§Ζ¥±»άΐΚ·îΒ(sh®¥)ΒΡàDœσ≤ΜΩ…Ρή≈cxίSœύΫΜ��Θ§“≤≤ΜΩ…Ρή≈cyίSœύΫΜΘ§ΒΪκS÷χxüoœό‘ω¥σΜρ «üoœό€p…Ό����Θ§Κ·îΒ(sh®¥)÷ΒüoœόΎÖΫϋ”Ύ0��Θ§Ι àDœώüoœόΫ”Ϋϋ”ΎxίS���ΓΘ
…φΦΑΫΜϋc«ι¦r
Γω ’“ΫΜϋcΦΑΫΜϋc²ÄîΒ(sh®¥)ΘΚ“―÷ΣΫΜϋcΒΡΡ≥“ΜôMΉχ‰Υ��Θ§¥ζ»κΦ¥Ω…«σ≥ωΤδΩvΉχ‰ΥΘ§Ζ¥÷°“ύ»Μ;°î“Σ«σΫΜϋcΉχ‰Υïr����Θ§¨ΔΖ¥±»άΐΚ·îΒ(sh®¥)≈c“Μ¥ΈΚ·îΒ(sh®¥)¬™(li®Δn)ΝΔΖΫ≥ΧΫM�Θ§ΏM––«σΫβ;
Γω «σΫβΫΜϋc²ÄîΒ(sh®¥)ΘΚ¨Δ“Μ¥ΈΚ·îΒ(sh®¥)ΚΆΖ¥±»άΐΚ·îΒ(sh®¥)¬™(li®Δn)ΝΔΖΫ≥ΧΫMΒΡΫβΒΡ²ÄîΒ(sh®¥)ΨΆ «ΫΜϋc²ÄîΒ(sh®¥)���ΓΘ
Γω «σΫβΈω ΫΘΚ«σΫβΈω Ϋ“ΜΑψ–η“ΣΚ·îΒ(sh®¥)àDœώ…œΒΡϋcΒΡΉχ‰Υ�Θ§Κ·îΒ(sh®¥)àDœώ…œ”–éΉ²ÄΈ¥÷ΣîΒ(sh®¥)Θ§“ΜΑψ–η“Σ’“?gu®©)Ή²Äϋc���ΓΘΖ¥±»άΐΚ·îΒ(sh®¥)ΒΡΨCΚœëΣ”Ο÷–Θ§Ά®≥Θ¨Λ’“ΫΜϋcΒΡΉχ‰Υ���Θ§èΡΕχΒΟ≥ωΫβΈω Ϋ≤ΔΖ÷³e«σΒΟΫβΈω Ϋ÷–ΒΡ≥ΘîΒ(sh®¥)÷Β����ΓΘ
…φΦΑΟφΖeΒΡΏ\”Ο
Ήχ‰ΥœΒ÷–ΒΡàD–ΈΟφΖeÜ•ν}ΉνΜυ±ΨΒΡàD–Έûι»ΐΫ«–Έ����Θ§Ϋβ¥πΚΥ–Ρ «“ΣΑ―ϋcΉχ‰ΥόD(zhu®Θn)Μ·ûιΨÄΕΈιLΕ»ΓΘ
®΄ »τ»ΐΫ«–Έ”–“ΜΏÖ‘ΎΉχ‰ΥίS…œ����Θ§Ά®≥Θ“‘Ώ@½lΏÖΉςûι»ΐΫ«–ΈΒΡΒΉΏÖ�ΓΘ
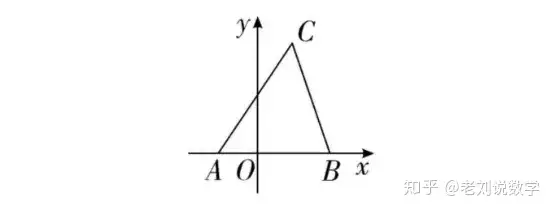
®΄ »ΐΏÖΕΦ≤Μ‘ΎΉχ‰ΥίS…œ�����Θ§–η“Σ¨ΠàD–ΈΏM––Ην―a�����ΓΘ
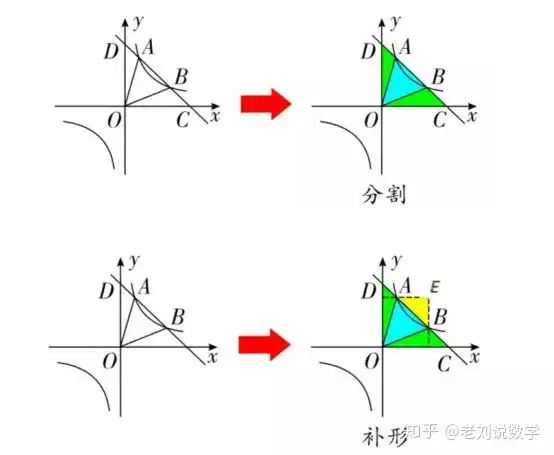
®΄ ‘Ύ«ΑΈΡ–‘Ό|(zh®§)1ΚΆ2÷–�����Θ§Έ“²ÉΧαΒΫ”–ξPΖ¥±»άΐΚ·îΒ(sh®¥)ΟφΖeΒΡ–‘Ό|(zh®§)��Θ§¥ΥΆβ�����Θ§Έ“²É–η“ΣΝΥΫβΒΡ «”–ξPΖ¥±»άΐΚ·îΒ(sh®¥)y=k/x(kûι≥ΘîΒ(sh®¥)«“k≠0)÷–|k|ΒΡéΉΚΈ“βΝxΘΚΏ^κp«ζΨÄ…œ»Έ“β“Μϋc“ΐxίS����ΓΔyίSΒΡ¥ΙΨÄΘ§ΥυΒΟΒΡΨΊ–ΈΟφΖeûι|k|�ΓΘ
®΄ »γΙϊν}ΡΩ÷–Ϋo≥ωΨÄΕΈ±»άΐΚΆΥΡΏÖ–ΈΒΡΟφΖe«σkÜ•ν}Θ§άϊ”ΟΆ§ΒΉΒ»ΗΏ»ΐΫ«–ΈΟφΖe≈cΗΏ÷°ιgΒΡξPœΒΘ§“‘ΦΑΟφΖe≈ck÷°ιgΒΡξPœΒ�Θ§«σ≥ωk�ΓΘ
ΉΔ“βΘΚΖ¥±»άΐΚ·îΒ(sh®¥)àDœσ «“ΜΖNΧΊ βΒΡàD–ΈΘ§ΥϋΒΡÉ…²ÄΖ÷÷ßΦ»ξP”Ύ‘≠ϋc¨ΠΖQ��Θ§”÷ξP”Ύ÷±ΨÄY=X�ΓΔY=-X¨ΠΖQΘ§“ρ¥ΥΈ“²ÉΉων}ïr“Σ≥δΖ÷άϊ”ΟΖ¥±»άΐΚ·îΒ(sh®¥)ΒΡ¨ΠΖQ–‘¹μΫβν}����ΓΘ
Ζ¥±»άΐΚ·îΒ(sh®¥)ΒΡ¥φ‘ΎΗ–‰OèäΘ§îΒ(sh®¥)¨WΩΦ‘΅÷–Μυ±ΨΡξΡξïΰ”ωΒΫΥϋ����Θ§ 딦Τδ–‘Ό|(zh®§)≤Δλ`ΜνΏ\”Ο «Ϋβν}ΒΡξPφIΓΘΈ“²É“Σ¨Π¥Υ“ΐΤπ÷Ί“ï�ΓΘ
ΓΓΓΓ ög”≠ Ι”Ο ÷ôCΓΔΤΫΑεΒ»“Τ³”‘O²δ‘LÜ•÷–ΩΦΨW(w®Θng)��Θ§2024÷–ΩΦ“Μ¬Ζ≈ψΑιΆ§––��ΘΓ>>ϋc™τ≤ιΩ¥