(Т»)әҜ”ө(shЁҙ)Update
1ЎўЧғБҝЈәФЪТ»ӮҖ(gЁЁ)Чғ»ҜЯ^іМЦРҝЙТФИЎІ»Н¬”ө(shЁҙ)ЦөөДБҝ�ЎЈ
іЈБҝЈәФЪТ»ӮҖ(gЁЁ)Чғ»ҜЯ^іМЦРЦ»ДЬИЎН¬Т»”ө(shЁҙ)ЦөөДБҝЎЈ
2��ЎўәҜ”ө(shЁҙ)ЈәТ»°гөД�Ј¬ФЪТ»ӮҖ(gЁЁ)Чғ»ҜЯ^іМЦРЈ¬Из№ыУРғЙӮҖ(gЁЁ)ЧғБҝxәНy�Ј¬ІўЗТҢҰУЪxөДГҝТ»ӮҖ(gЁЁ)ҙ_¶ЁөДЦөЈ¬y¶јУРОЁТ»ҙ_¶ЁөДЦөЕcЖдҢҰ‘Ә(yЁ©ng)��Ј¬ДЗГҙОТӮғҫН°Сx·QһйЧФЧғБҝ���Ј¬°Сy·QһйТтЧғБҝ��Ј¬yКЗxөДәҜ”ө(shЁҙ)�ЎЈ
*ЕР”аYКЗ·сһйXөДәҜ”ө(shЁҙ)��Ј¬Ц»ТӘҝҙXИЎЦөҙ_¶ЁөД•r(shЁӘ)әт�Ј¬YКЗ·сУРОЁТ»ҙ_¶ЁөДЦөЕcЦ®ҢҰ‘Ә(yЁ©ng)
3Ўў¶ЁБxУтЈәТ»°гөД�Ј¬Т»ӮҖ(gЁЁ)әҜ”ө(shЁҙ)өДЧФЧғБҝФКФSИЎЦөөД·¶ҮъЈ¬ҪРЧцЯ@ӮҖ(gЁЁ)әҜ”ө(shЁҙ)өД¶ЁБxУт���ЎЈ
4��Ўўҙ_¶ЁәҜ”ө(shЁҙ)¶ЁБxУтөД·Ҫ·ЁЈә
(1)кP(guЁЎn)ПөКҪһйХыКҪ•r(shЁӘ)��Ј¬әҜ”ө(shЁҙ)¶ЁБxУт?yЁӨn)йИ«уwҢҚ(shЁӘ)”ө(shЁҙ);
(2)кP(guЁЎn)ПөКҪә¬УР·ЦКҪ•r(shЁӘ)���Ј¬·ЦКҪөД·ЦДёІ»өИУЪБг;
(3)кP(guЁЎn)ПөКҪә¬УР¶юҙОёщКҪ•r(shЁӘ)���Ј¬ұ»й_·Е·Ҫ”ө(shЁҙ)ҙуУЪөИУЪБг;
(4)кP(guЁЎn)ПөКҪЦРә¬УРЦё”ө(shЁҙ)һйБгөДКҪЧУ•r(shЁӘ)Ј¬өЧ”ө(shЁҙ)І»өИУЪБг;
(5)ҢҚ(shЁӘ)лHҶ–о}ЦР��Ј¬әҜ”ө(shЁҙ)¶ЁБxУтЯҖТӘәНҢҚ(shЁӘ)лHЗйӣrПа·ыәП�Ј¬К№Ц®УРТвБxЎЈ
5�ЎўәҜ”ө(shЁҙ)өДҪвОцКҪЈәУГә¬УРұнКҫЧФЧғБҝөДЧЦДёөДҙъ”ө(shЁҙ)КҪұнКҫТтЧғБҝөДКҪЧУҪРЧцәҜ”ө(shЁҙ)өДҪвОцКҪ
6���ЎўәҜ”ө(shЁҙ)өДҲDПс
Т»°гҒнХf���Ј¬ҢҰУЪТ»ӮҖ(gЁЁ)әҜ”ө(shЁҙ)Ј¬Из№ы°СЧФЧғБҝЕcәҜ”ө(shЁҙ)өДГҝҢҰҢҰ‘Ә(yЁ©ng)Цө·Ц„eЧчһйьc(diЁЈn)өДҷM���ЎўҝvЧшҳЛ(biЁЎo)�Ј¬ДЗГҙЧшҳЛ(biЁЎo)ЖҪГжғИ(nЁЁi)УЙЯ@Р©ьc(diЁЈn)ҪMіЙөДҲDРОЈ¬ҫНКЗЯ@ӮҖ(gЁЁ)әҜ”ө(shЁҙ)өДҲDПу.
7�ЎўГиьc(diЁЈn)·Ё®ӢәҜ”ө(shЁҙ)ҲDРОөДТ»°гІҪуE
өЪТ»ІҪЈәБРұн(ұнЦРҪoіцТ»Р©ЧФЧғБҝөДЦөј°ЖдҢҰ‘Ә(yЁ©ng)өДәҜ”ө(shЁҙ)Цө);
өЪ¶юІҪЈәГиьc(diЁЈn)(ФЪЦұҪЗЧшҳЛ(biЁЎo)ПөЦРЈ¬ТФЧФЧғБҝөДЦөһйҷMЧшҳЛ(biЁЎo)��Ј¬Па‘Ә(yЁ©ng)өДәҜ”ө(shЁҙ)ЦөһйҝvЧшҳЛ(biЁЎo)���Ј¬ГиіцұнёсЦР”ө(shЁҙ)ЦөҢҰ‘Ә(yЁ©ng)өДёчьc(diЁЈn));
өЪИэІҪЈәЯBҫҖ(°ҙХХҷMЧшҳЛ(biЁЎo)УЙРЎөҪҙуөДнҳРт°СЛщГиіцөДёчьc(diЁЈn)УГЖҪ»¬ЗъҫҖЯBҪУЖрҒн)�ЎЈ
8���ЎўәҜ”ө(shЁҙ)өДұнКҫ·Ҫ·Ё
БРұн·ЁЈәТ»ДҝБЛИ»���Ј¬К№УГЖрҒн·ҪұгЈ¬ө«БРіцөДҢҰ‘Ә(yЁ©ng)ЦөКЗУРПЮөД���Ј¬І»ТЧҝҙіцЧФЧғБҝЕcәҜ”ө(shЁҙ)Ц®йgөДҢҰ‘Ә(yЁ©ng)ТҺ(guЁ©)ВЙ���ЎЈ
ҪвОцКҪ·ЁЈәәҶҶОГчБЛЈ¬ДЬүтңК(zhЁіn)ҙ_өШ·ҙУіХыӮҖ(gЁЁ)Чғ»ҜЯ^іМЦРЧФЧғБҝЕcәҜ”ө(shЁҙ)Ц®йgөДПаТАкP(guЁЎn)Пө��Ј¬ө«УРР©ҢҚ(shЁӘ)лHҶ–о}ЦРөДәҜ”ө(shЁҙ)кP(guЁЎn)Пө��Ј¬І»ДЬУГҪвОцКҪұнКҫ���ЎЈ
ҲDПу·ЁЈәРОПуЦұУ^���Ј¬ө«Ц»ДЬҪьЛЖөШұнЯ_(dЁў)ғЙӮҖ(gЁЁ)ЧғБҝЦ®йgөДәҜ”ө(shЁҙ)кP(guЁЎn)Пө��ЎЈ
(¶ю)Т»ҙОәҜ”ө(shЁҙ)Update
1�ЎўТ»ҙОәҜ”ө(shЁҙ)өД¶ЁБx
Т»°гөШ���Ј¬РОИз
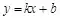
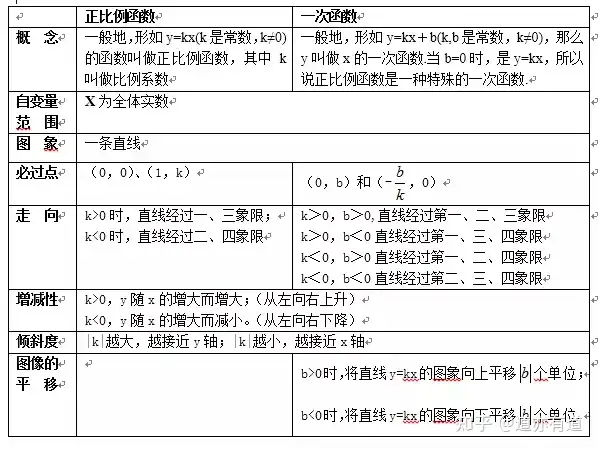
(k���Ј¬bКЗіЈ”ө(shЁҙ)Ј¬ЗТk≠0)өДәҜ”ө(shЁҙ)�Ј¬ҪРЧцТ»ҙОәҜ”ө(shЁҙ)Ј¬ЖдЦРxКЗЧФЧғБҝ��ЎЈ®”(dЁЎng)b=0•r(shЁӘ)���Ј¬Т»ҙОәҜ”ө(shЁҙ)y=kx��Ј¬УЦҪРЧцХэұИАэәҜ”ө(shЁҙ)ЎЈ
ўЕТ»ҙОәҜ”ө(shЁҙ)өДҪвОцКҪөДРОКҪКЗ
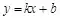
�Ј¬ТӘЕР”аТ»ӮҖ(gЁЁ)әҜ”ө(shЁҙ)КЗ·сКЗТ»ҙОәҜ”ө(shЁҙ)Ј¬ҫНКЗЕР”аКЗ·сДЬ»ҜіЙТФЙПРОКҪ.
ўЖ®”(dЁЎng)b=0���Ј¬k≠0•r(shЁӘ)��Ј¬y=kxИФКЗТ»ҙОәҜ”ө(shЁҙ).
ўЗ®”(dЁЎng)k=0���Ј¬b≠0•r(shЁӘ)���Ј¬ЛьІ»КЗТ»ҙОәҜ”ө(shЁҙ).
ўИХэұИАэәҜ”ө(shЁҙ)КЗТ»ҙОәҜ”ө(shЁҙ)өДМШАэЈ¬Т»ҙОәҜ”ө(shЁҙ)°ьАЁХэұИАэәҜ”ө(shЁҙ).
2��ЎўХэұИАэәҜ”ө(shЁҙ)ј°РФЩ|(zhЁ¬)
Т»°гөШ���Ј¬РОИзy=kx(kКЗіЈ”ө(shЁҙ)��Ј¬k≠0)өДәҜ”ө(shЁҙ)ҪРЧцХэұИАэәҜ”ө(shЁҙ)�Ј¬ЖдЦРkҪРЧцұИАэПө”ө(shЁҙ).
ЧўЈә
ХэұИАэәҜ”ө(shЁҙ)Т»°гРОКҪ y=kx (kІ»һйБг)
ўЩ kІ»һйБг ўЪ xЦё”ө(shЁҙ)һй1 ўЫ bИЎБг
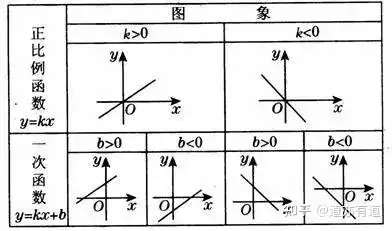
®”(dЁЎng)k>0•r(shЁӘ)�Ј¬ЦұҫҖy=kxҪӣ(jЁ©ng)Я^Т»ЎўИэПуПЮ���Ј¬ҸДЧуПтУТЙПЙэ�Ј¬јҙлSxөДФцҙуyТІФцҙу;
®”(dЁЎng)k<0•r(shЁӘ)�Ј¬ЦұҫҖy=kxҪӣ(jЁ©ng)Я^¶юЎўЛДПуПЮ�Ј¬ҸДЧуПтУТПВҪө�Ј¬јҙлSxФцҙуy·ҙ¶шңpРЎ.
(1) ҪвОцКҪЈәy=kx(kКЗіЈ”ө(shЁҙ)�Ј¬k≠0)
(2) ұШЯ^ьc(diЁЈn)Јә(0Ј¬0)���Ўў(1�Ј¬k)
(3) ЧЯПтЈәk>0•r(shЁӘ)��Ј¬ҲDПсҪӣ(jЁ©ng)Я^Т»�ЎўИэПуПЮ;k<0•r(shЁӘ)Ј¬ҲDПсҪӣ(jЁ©ng)Я^
¶ю��ЎўЛДПуПЮ
(4) ФцңpРФЈәk>0�Ј¬yлSxөДФцҙу¶шФцҙу;k<0Ј¬yлSxФцҙу¶шңpРЎ
(5) ғAРұ¶ИЈә|k|ФҪҙу�Ј¬ФҪҪУҪьyЭS;|k|ФҪРЎЈ¬ФҪҪУҪьxЭS
3�ЎўТ»ҙОәҜ”ө(shЁҙ)ј°РФЩ|(zhЁ¬)
Т»°гөШЈ¬РОИзy=kx+b(k,bКЗіЈ”ө(shЁҙ)���Ј¬k≠0)��Ј¬ДЗГҙyҪРЧцxөДТ»ҙОәҜ”ө(shЁҙ).®”(dЁЎng)b=0•r(shЁӘ)�Ј¬y=kx+bјҙy=kx���Ј¬ЛщТФХfХэұИАэәҜ”ө(shЁҙ)КЗТ»·NМШКвөДТ»ҙОәҜ”ө(shЁҙ).
ЧўЈәТ»ҙОәҜ”ө(shЁҙ)Т»°гРОКҪ y=kx+b (kІ»һйБг)
ўЩ kІ»һйБг
ўЪxЦё”ө(shЁҙ)һй1
ўЫ bИЎИОТвҢҚ(shЁӘ)”ө(shЁҙ)
Т»ҙОәҜ”ө(shЁҙ)y=kx+bөДҲDПуКЗҪӣ(jЁ©ng)Я^(0�Ј¬b)әН(-b/k���Ј¬0)ғЙьc(diЁЈn)өДТ»—lЦұҫҖ��Ј¬ОТӮғ·QЛьһйЦұҫҖy=kx+b,ЛьҝЙТФҝҙЧчУЙЦұҫҖy=kxЖҪТЖ|b|ӮҖ(gЁЁ)ҶОО»йL¶ИөГөҪ.(®”(dЁЎng)b>0•r(shЁӘ)�Ј¬ПтЙПЖҪТЖ;®”(dЁЎng)b<0•r(shЁӘ)�Ј¬ПтПВЖҪТЖ)
(1)ҪвОцКҪЈәy=kx+b(kЎўbКЗіЈ”ө(shЁҙ)�Ј¬k≠0)
(2)ұШЯ^ьc(diЁЈn)Јә(0Ј¬b)әН(-b/k���Ј¬0)
(3)ЧЯПтЈә
k>0��Ј¬ҲDПуҪӣ(jЁ©ng)Я^өЪТ»��ЎўИэПуПЮ;k<0�Ј¬ҲDПуҪӣ(jЁ©ng)Я^өЪ¶ю���ЎўЛДПуПЮ
b>0��Ј¬ҲDПуҪӣ(jЁ©ng)Я^өЪТ»���Ўў¶юПуПЮ;b<0���Ј¬ҲDПуҪӣ(jЁ©ng)Я^өЪИэЎўЛДПуПЮ
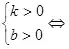
ЦұҫҖҪӣ(jЁ©ng)Я^өЪТ»��Ўў¶ю���ЎўИэПуПЮ
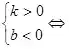
ЦұҫҖҪӣ(jЁ©ng)Я^өЪТ»���ЎўИэЎўЛДПуПЮ
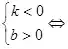
ЦұҫҖҪӣ(jЁ©ng)Я^өЪТ»���Ўў¶ю���ЎўЛДПуПЮ
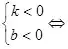
ЦұҫҖҪӣ(jЁ©ng)Я^өЪ¶юЎўИэ�ЎўЛДПуПЮ
(4)ФцңpРФЈә k>0Ј¬yлSxөДФцҙу¶шФцҙу;k<0���Ј¬yлSxФцҙу¶шңpРЎ.
(5)ғAРұ¶ИЈә|k|ФҪҙу�Ј¬ҲDПуФҪҪУҪьУЪyЭS;|k|ФҪРЎЈ¬ҲDПуФҪҪУҪьУЪxЭS.
(6)ҲDПсөДЖҪТЖЈә
®”(dЁЎng)b>0•r(shЁӘ)�Ј¬ҢўЦұҫҖy=kxөДҲDПуПтЙПЖҪТЖbӮҖ(gЁЁ)ҶОО»;
®”(dЁЎng)b<0•r(shЁӘ)Ј¬ҢўЦұҫҖy=kxөДҲDПуПтПВЖҪТЖbӮҖ(gЁЁ)ҶОО».
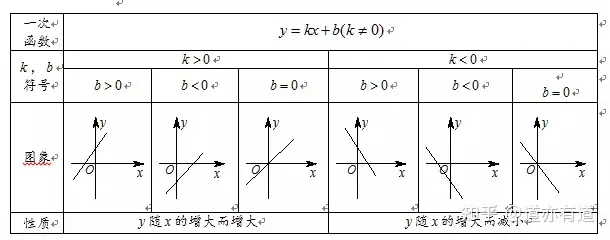
4�ЎўТ»ҙОәҜ”ө(shЁҙ)y=kx+bөДҲDПуөД®Ӣ·Ё.
ёщ“ю(jЁҙ)ҺЧәОЦӘЧR(shЁӘ)ЈәҪӣ(jЁ©ng)Я^ғЙьc(diЁЈn)ДЬ®ӢіцТ»—lЦұҫҖ���Ј¬ІўЗТЦ»ДЬ®ӢіцТ»—lЦұҫҖ���Ј¬јҙғЙьc(diЁЈn)ҙ_¶ЁТ»—lЦұҫҖЈ¬ЛщТФ®ӢТ»ҙОәҜ”ө(shЁҙ)өДҲDПу•r(shЁӘ)���Ј¬Ц»ТӘПИГиіцғЙьc(diЁЈn)��Ј¬ФЩЯBіЙЦұҫҖјҙҝЙ.Т»°гЗйӣrПВЈәКЗПИЯxИЎЛьЕcғЙЧшҳЛ(biЁЎo)ЭSөДҪ»ьc(diЁЈn)Јә(0��Ј¬b)���Ј¬(-b/kЈ¬0) .јҙҷMЧшҳЛ(biЁЎo)»тҝvЧшҳЛ(biЁЎo)һй0өДьc(diЁЈn).
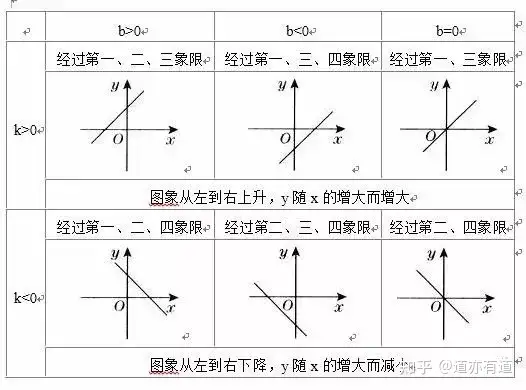
5�ЎўХэұИАэәҜ”ө(shЁҙ)ЕcТ»ҙОәҜ”ө(shЁҙ)Ц®йgөДкP(guЁЎn)ПөЈәТ»ҙОәҜ”ө(shЁҙ)y=kx+bөДҲDПуКЗТ»—lЦұҫҖЈ¬ЛьҝЙТФҝҙЧчКЗУЙЦұҫҖy=kxЖҪТЖ|b|ӮҖ(gЁЁ)ҶОО»йL¶И¶шөГөҪ(®”(dЁЎng)b>0•r(shЁӘ)���Ј¬ПтЙПЖҪТЖ;®”(dЁЎng)b<0•r(shЁӘ)���Ј¬ПтПВЖҪТЖ)
6���ЎўХэұИАэәҜ”ө(shЁҙ)әНТ»ҙОәҜ”ө(shЁҙ)ј°РФЩ|(zhЁ¬)
6ЎўЦұҫҖ
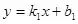
(
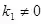
)Еc
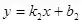
(
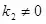
)өДО»ЦГкP(guЁЎn)Пө
(1)ғЙЦұҫҖЖҪРР
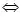
ЗТ
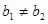
(2)ғЙЦұҫҖПаҪ»
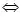
(3)ғЙЦұҫҖЦШәП
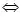
ЗТ
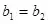
(4)ғЙЦұҫҖҙ№Цұ
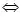
7�ЎўУГҙэ¶ЁПө”ө(shЁҙ)·Ёҙ_¶ЁәҜ”ө(shЁҙ)ҪвОцКҪөДТ»°гІҪуEЈә
(1)ёщ“ю(jЁҙ)ТСЦӘ—lјюҢ‘іцә¬УРҙэ¶ЁПө”ө(shЁҙ)өДәҜ”ө(shЁҙ)кP(guЁЎn)ПөКҪ;
(2)ҢўxЎўyөДҺЧҢҰЦө»тҲDПуЙПөДҺЧӮҖ(gЁЁ)ьc(diЁЈn)өДЧшҳЛ(biЁЎo)ҙъИлЙПКцәҜ”ө(shЁҙ)кP(guЁЎn)ПөКҪЦРөГөҪТФҙэ¶ЁПө”ө(shЁҙ)һйОҙЦӘ”ө(shЁҙ)өД·ҪіМ;
(3)Ҫв·ҪіМөГіцОҙЦӘПө”ө(shЁҙ)өДЦө;
(4)ҢўЗуіцөДҙэ¶ЁПө”ө(shЁҙ)ҙъ»ШЛщЗуөДәҜ”ө(shЁҙ)кP(guЁЎn)ПөКҪЦРөГіцЛщЗуәҜ”ө(shЁҙ)өДҪвОцКҪ.
°l(fЁЎ)ІјУЪ 2021-10-25 18:49
ЎЎЎЎ ҡgУӯК№УГКЦҷC(jЁ©)��ЎўЖҪ°еөИТЖ„У(dЁ°ng)ФO(shЁЁ)ӮдФLҶ–ЦРҝјҫW(wЁЈng)��Ј¬2023ЦРҝјТ»В·Ег°йН¬РР�ЈЎ>>ьc(diЁЈn)“фІйҝҙ













