證明三角形對稱的性質(zhì)

　　根據(jù)等腰三角形的對稱性還應(yīng)有如下重要的性質(zhì)，雖在證明中不能直接引用，但對于填空、選擇則可直接運(yùn)用，并且這些性質(zhì)對今后的推理證明都有非常重要的作用。

　　①等腰三角形兩腰上的中線相等

　　已知：在ΔABC 中，AB＝AC，若BD，CE分別是AC，AB邊上的中線，則有BD＝CE。

　　

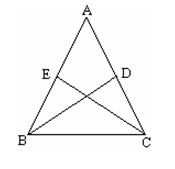
　　證明：∵BD，CE是AB，AC邊上的中線(已知)

　　∴AD＝ AC，AE＝ AB(中線定義)

　　∵AB＝AC(已知)

　　∴AD＝AE

　　在ΔABD和ΔACE中，

　　∴ΔABD≌ΔACE(SAS)

　　∴BD＝CE(全等三角形對應(yīng)邊相等)。

　　②等腰三角形兩腰上的高相等

　　已知：在ΔABC中，AB＝AC，如果BD，CE分別是AC，AB邊上的高，那么BD＝CE。

　　同學(xué)可以試著證明一下，還用全等三角形去證。

　　③等腰三角形兩底角的平分線相等

　　已知：在ΔABC中，AB＝AC，如果BD，CE分別是∠ABC和∠ACB的平分線，那么BD＝CE。

　　同學(xué)可利用全等三角形法證明。


 

　　 歡迎使用手機(jī)、平板等移動設(shè)備訪問中考網(wǎng)，2024中考一路陪伴同行！>>點(diǎn)擊查看