į┌šnā╚(n©©i)╬ęéāīW(xu©”)▀^┴╦╣┤╣╔Č©└Ē╝░╦³Ą──µČ©└ĒŻ«
ĪĪĪĪ╣┤╣╔Č©└Ē ų▒ĮŪ╚²ĮŪą╬ā╔ų▒ĮŪ▀ģa����Ż¼bĄ─ŲĮĘĮ║═Ą╚ė┌ą▒▀ģcĄ─ŲĮĘĮŻ¼╝┤
a2+b2=c2Ż«
ĪĪĪĪ╣┤╣╔Č©└Ē─µČ©└Ē ╚ń╣¹╚²ĮŪą╬╚²▀ģķLa�Ż¼b�����Ż¼cėąŽ┬├µĻP(gu©Īn)ŽĄŻ║
a2+b2=c2
ĪĪĪĪ─Ū├┤▀@éĆ╚²ĮŪą╬╩Ūų▒ĮŪ╚²ĮŪą╬Ż«
ĪĪĪĪįńį┌3000─ĻŪ░���Ż¼╬ęć°ęčėąĪ░╣┤ÅV╚²���Ż¼╣╔ą▐╦─�Ż¼ÅĮĻ¢╬ÕĪ▒Ą─šfĘ©Ż«
ĪĪĪĪĻP(gu©Īn)ė┌╣┤╣╔Č©└Ē�����Ż¼ėą║▄ČÓūCĘ©Ż¼į┌╬ęć°╦³éāČ╝╩Ūė├Ų┤łDą╬├µĘeĘĮĘ©üĒūC├„Ą─Ż«Ž┬├µĄ─ūCĘ©1╩ŪÜWÄū└’Ą├ūCĘ©Ż«
ĪĪĪĪūCĘ©1 ╚ńłD2-16╦∙╩ŠŻ«į┌RtĪ„ABCĄ─═Ōé╚(c©©)�����Ż¼ęįĖ„▀ģ×ķ▀ģķLĘųäeū„š²ĘĮą╬ABDEŻ¼BCHK���Ż¼ACFGŻ¼╦³éāĄ─├µĘeĘųäe╩Ūc2��Ż¼a2Ż¼b2Ż«Ž┬├µūC├„�Ż¼┤¾š²ĘĮą╬Ą─├µĘeĄ╚ė┌ā╔éĆąĪš²ĘĮą╬Ą─├µĘeų«║═Ż«
ĪĪĪĪ▀^Cę²CMĪ╬BD����Ż¼Į╗ABė┌L���Ż¼▀BĮėBG�Ż¼CEŻ«ę“×ķ
AB=AEŻ¼AC=AG���Ż¼ĪŽCAE=ĪŽBAGŻ¼
ĪĪĪĪ╦∙ęįĪ„ACEĪšĪ„AGB(SAS)Ż«Č°

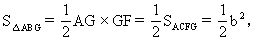 ĪĪ
ĪĪ

ĪĪĪĪ╦∙ęį SAEML=b2Ż« ó┘
ĪĪĪĪ═¼└Ē┐╔ūC SBLMD=a2Ż« ó┌
ĪĪĪĪó┘+ó┌Ą├
SABDE=SAEML+SBLMD=b2+a2��Ż¼
ĪĪĪĪ╝┤ c2=a2+b2Ż«
ĪĪĪĪūCĘ©2 ╚ńłD2-17╦∙╩ŠŻ«īóRtĪ„ABCĄ─ā╔Ślų▒ĮŪ▀ģCA�Ż¼CBĘųäečėķLĄĮD�Ż¼F�Ż¼╩╣AD=a���Ż¼BF=bŻ«═Ļ│╔š²ĘĮą╬CDEF(╦³Ą─▀ģķL×ķa+b)�Ż¼ėųį┌DE╔ŽĮž╚ĪDG=bŻ¼į┌EF╔ŽĮž╚ĪEH=b�Ż¼▀BĮėAG����Ż¼GHŻ¼HBŻ«ė╔ū„łDęūų¬
Ī„ADGĪšĪ„GEHĪšĪ„HFBĪšĪ„ABC����Ż¼
ĪĪĪĪ╦∙ęį
ĪĪĪĪAG=GH=HB=AB=cŻ¼
ĪĪĪĪĪŽBAG=ĪŽAGH=ĪŽGHB=ĪŽHBA=90ĪŃ��Ż¼
ĪĪĪĪę“┤╦�����Ż¼AGHB×ķ▀ģķL╩ŪcĄ─š²ĘĮą╬Ż«’@╚╗Ż¼š²ĘĮą╬CDEFĄ─├µĘeĄ╚ė┌š²ĘĮą╬AGHBĄ─├µĘe┼c╦─éĆ╚½Ą╚Ą─ų▒ĮŪ╚²ĮŪą╬(Ī„ABC�Ż¼Ī„ADG��Ż¼Ī„GEHŻ¼Ī„HFB)Ą─├µĘe║═�Ż¼╝┤

ĪĪĪĪ╗»║åĄ├ a2+b2=c2Ż«

 ĪĪ
ĪĪ
ĪĪĪĪūCĘ©3 ╚ńłD2-18Ż«į┌ų▒ĮŪ╚²ĮŪą╬ABCĄ─ą▒▀ģAB╔ŽŽ“═Ōū„š²ĘĮą╬ABDE�Ż¼čėķLCB�Ż¼ūįEū„EGĪ═CBčėķLŠĆė┌G���Ż¼ūįDū„DKĪ═CBčėķLŠĆė┌K�Ż¼ėųū„AF�����Ż¼ DHĘųäe┤╣ų▒EGė┌FŻ¼HŻ«ė╔ū„łD▓╗ļyūC├„�Ż¼Ž┬╩÷Ė„ų▒ĮŪ╚²ĮŪą╬Š∙┼cRtĪ„ABC╚½Ą╚Ż║
Ī„AFEĪšĪ„EHDĪšĪ„BKDĪšĪ„ACBŻ«
ĪĪĪĪįO(sh©©)╬Õ▀ģą╬ACKDEĄ─├µĘe×ķS�Ż¼ę╗ĘĮ├µ
ĪĪĪĪS=SABDE+2SĪ„ABC�Ż¼ ó┘
ĪĪĪĪ┴Ēę╗ĘĮ├µ
ĪĪĪĪS=SACGF+SHGKD+2SĪ„ABCŻ« ó┌
ĪĪĪĪė╔ó┘Ż¼ó┌
ĪĪĪĪ
ĪĪĪĪ╦∙ęį c2=a2+b2Ż«
ĪĪĪĪĻP(gu©Īn)ė┌╣┤╣╔Č©└Ē�Ż¼į┌╬ęć°╣┼┤·▀Ćėą║▄ČÓŅÉ╦Ų╔Ž╩÷Ų┤łDŪ¾ĘeĄ─ūC├„ĘĮĘ©�Ż¼╬ęéāīóį┌┴Ģ(x©¬)Ņ}ųąš╣╩ŠŲõųąę╗ąĪ▓┐Ęų���Ż¼╦³éāČ╝ęįųąć°╣┼┤·öĄ(sh©┤)īW(xu©”)╝ęĄ─├¹ūų├³├¹Ż«
ĪĪĪĪ└¹ė├╣┤╣╔Č©└Ē�����Ż¼į┌ę╗░Ń╚²ĮŪą╬ųą�����Ż¼┐╔ęįĄ├ĄĮę╗éĆĖ³ę╗░ŃĄ─ĮY(ji©”)šōŻ«
ĪĪĪĪČ©└Ē į┌╚²ĮŪą╬ųą��Ż¼õJĮŪ(╗“ŌgĮŪ)╦∙ī”Ą─▀ģĄ─ŲĮĘĮĄ╚ė┌┴Ē═Ōā╔▀ģĄ─ŲĮĘĮ║═��Ż¼£p╚ź(╗“╝ė╔Ž)▀@ā╔▀ģųąĄ─ę╗▀ģ┼c┴Ēę╗▀ģį┌▀@▀ģ(╗“ŲõčėķLŠĆ)╔ŽĄ─╔õė░Ą─│╦ĘeĄ─2▒ČŻ«

ĪĪĪĪūC (1)įO(sh©©)ĮŪC×ķõJĮŪ���Ż¼╚ńłD2-19╦∙╩ŠŻ«ū„ADĪ═BCė┌DŻ¼ ätCDŠ═╩ŪACį┌BC╔ŽĄ─╔õė░Ż«į┌ų▒ĮŪ╚²ĮŪą╬ABDųą�Ż¼
ĪĪĪĪAB2=AD2+BD2Ż¼ ó┘
ĪĪĪĪį┌ų▒ĮŪ╚²ĮŪą╬ACDųą��Ż¼
ĪĪĪĪAD2=AC2-CD2�Ż¼ ó┌
ĪĪĪĪėų
ĪĪĪĪBD2=(BC-CD)2Ż¼ ó█
ĪĪĪ�����Īó┌���Ż¼ó█┤·╚ļó┘Ą├
ĪĪĪĪAB2=(AC2-CD2)+(BC-CD)2
ĪĪĪĪĪĪ=AC2-CD2+BC2+CD2-2BC?CD
ĪĪĪĪĪĪ=AC2+BC2-2BC?CD�Ż¼
ĪĪĪĪ╝┤
ĪĪĪĪc2=a2+b2-2a?CDŻ« ó▄
ĪĪĪĪ(2)įO(sh©©)ĮŪC×ķŌgĮŪŻ¼╚ńłD2-20╦∙╩ŠŻ«▀^Aū„AD┼cBCčėķLŠĆ┤╣ų▒ė┌D�����Ż¼ätCDŠ═╩ŪACį┌BC(čėķLŠĆ)╔ŽĄ─╔õė░Ż«į┌ų▒ĮŪ╚²ĮŪą╬ABDųą���Ż¼
ĪĪĪĪAB2=AD2+BD2�Ż¼ ó▌
ĪĪĪĪį┌ų▒ĮŪ╚²ĮŪą╬ACDųą��Ż¼

ĪĪĪĪAD2=AC2-CD2�����Ż¼ ó▐
ĪĪĪĪėų
ĪĪĪĪBD2=(BC+CD)2Ż¼ ó▀
ĪĪĪĪīóó▐Ż¼ó▀┤·╚ļó▌Ą├
ĪĪĪĪAB2=(AC2-CD2)+(BC+CD)2
ĪĪĪĪĪĪ=AC2-CD2+BC2+CD2+2BC?CD
ĪĪĪĪĪĪ=AC2+BC2+2BC?CD��Ż¼
ĪĪĪĪ╝┤
ĪĪĪĪc2=a2+b2+2a?cdŻ« óÓ
ĪĪĪĪŠC║Žó▄Ż¼óÓŠ═╩Ū╬ęéā╦∙ąĶꬥ─ĮY(ji©”)šō
ĪĪĪĪ
ĪĪĪĪ╠žäeĄž���Ż¼«ö(d©Īng)ĪŽC=90ĪŃĢrŻ¼CD=0�����Ż¼╔Ž╩÷ĮY(ji©”)šōš²╩Ū╣┤╣╔Č©└ĒĄ─▒Ē╩÷Ż║
c2=a2+b2Ż«
ĪĪĪĪę“┤╦�����Ż¼╬ęéā│ŻėųĘQ┤╦Č©└Ē×ķÅV╣┤╣╔Č©└Ē(ęŌ╦╝╩Ū╣┤╣╔Č©└Ēį┌ę╗░Ń╚²ĮŪą╬ųąĄ─═ŲÅV)Ż«
ĪĪĪĪė╔ÅV╣┤╣╔Č©└Ē╬ęéā┐╔ęįūį╚╗Ąž═Ųī¦(d©Żo)│÷╚²ĮŪą╬╚²▀ģĻP(gu©Īn)ŽĄī”ė┌ĮŪĄ─ė░ĒæŻ«į┌Ī„ABCųą�Ż¼
ĪĪĪĪ(1)╚¶c2=a2+b2��Ż¼ätĪŽC=90ĪŃŻ╗
ĪĪĪĪ(2)╚¶c2Ż╝a2+b2�����Ż¼ätĪŽCŻ╝90ĪŃŻ╗
ĪĪĪĪ(3)╚¶c2ŻŠa2+b2�Ż¼ätĪŽCŻŠ90ĪŃŻ«
ĪĪĪĪ╣┤╣╔Č©└Ē╝░ÅV╣┤╣╔Č©└Ē╔Ņ┐╠ĄžĮę╩Š┴╦╚²ĮŪą╬ā╚(n©©i)▓┐Ą─▀ģĮŪĻP(gu©Īn)ŽĄ���Ż¼ę“┤╦į┌ĮŌøQ╚²ĮŪą╬(╝░ČÓ▀ģą╬)Ą─å¢Ņ}ųąėąų°ÅVĘ║Ą─æ¬(y©®ng)ė├Ż«
ĪĪĪĪ└²1 ╚ńłD2-21╦∙╩ŠŻ«ęčų¬Ż║į┌š²ĘĮą╬ABCDųąŻ¼ĪŽBACĄ─ŲĮĘųŠĆĮ╗BCė┌E����Ż¼ū„EFĪ═ACė┌FŻ¼ū„FGĪ═ABė┌GŻ«Ū¾ūCŻ║AB2=2FG2Ż«

ĪĪĪĪĘų╬÷ ūóęŌĄĮš²ĘĮą╬Ą─╠žąįĪŽCAB=45ĪŃŻ¼╦∙ęįĪ„AGF╩ŪĄ╚č³ų▒ĮŪ╚²ĮŪą╬��Ż¼Å─Č°ėąAF2=2FG2�����Ż¼ę“Č°æ¬(y©®ng)ėąAF=AB�����Ż¼▀@åó░l(f©Ī)╬ęéā?n©©i)źūC├„Ī„ABEĪšĪ„AFEŻ«
ĪĪĪĪūC ę“×ķAE╩ŪĪŽFABĄ─ŲĮĘųŠĆ�Ż¼EFĪ═AF�Ż¼ėųAE╩ŪĪ„AFE┼cĪ„ABEĄ─╣½╣▓▀ģŻ¼╦∙ęį
RtĪ„AFEĪšRtĪ„ABE(AAS)�Ż¼
ĪĪĪĪ╦∙ęį AF=ABŻ« ó┘
ĪĪĪĪį┌RtĪ„AGFųą��Ż¼ę“×ķĪŽFAG=45ĪŃ�����Ż¼╦∙ęį
AG=FG�Ż¼
ĪĪĪĪAF2=AG2+FG2=2FG2Ż« ó┌
ĪĪĪĪė╔ó┘Ż¼ó┌Ą├
AB2=2FG2Ż«
ĪĪĪĪšf├„ ╩┬īŹ╔Ž�����Ż¼į┌īÅŅ}ųą�����Ż¼Śl╝■Ī░AEŲĮĘųĪŽBACĪ▒╝░Ī░EFĪ═ACė┌FĪ▒æ¬(y©®ng)╩╣╬ęéāęŌūRĄĮā╔éĆų▒ĮŪ╚²ĮŪą╬Ī„AFE┼cĪ„ABE╚½Ą╚�Ż¼Å─Č°īóABĪ░▀^Č╔Ī▒ĄĮAFŻ¼╩╣AF(╝┤AB)┼cFG╠Äė┌═¼ę╗éĆų▒ĮŪ╚²ĮŪą╬ųą���Ż¼┐╔ęį└¹ė├╣┤╣╔Č©└Ē▀M(j©¼n)ąąūC├„┴╦Ż«
ĪĪĪĪ└²2 ╚ńłD2-22╦∙╩ŠŻ«AM╩ŪĪ„ABCĄ─BC▀ģ╔ŽĄ─ųąŠĆ��Ż¼Ū¾ūCŻ║AB2+AC2=2(AM2+BM2)Ż«

ĪĪĪĪūC ▀^Aę²ADĪ═BCė┌D(▓╗Ę┴įO(sh©©)D┬õį┌▀ģBCā╚(n©©i))Ż«ė╔ÅV╣┤╣╔Č©└Ē����Ż¼į┌Ī„ABMųą��Ż¼
ĪĪĪĪAB2=AM2+BM2+2BM?MDŻ« ó┘
ĪĪĪĪį┌Ī„ACMųą�Ż¼
ĪĪĪĪAC2=AM2+MC2-2MC?MDŻ« ó┌
ĪĪĪĪó┘+ó┌Ż¼▓óūóęŌĄĮMB=MC�����Ż¼╦∙ęį
ĪĪĪĪAB2+AC2=2(AM2+BM2)Ż« ó█
ĪĪĪĪ╚ń╣¹įO(sh©©)Ī„ABC╚²▀ģķLĘųäe×ķaŻ¼b�Ż¼cŻ¼╦³éāī”æ¬(y©®ng)▀ģ╔ŽĄ─ųąŠĆķLĘųäe×ķma�����Ż¼mb�����Ż¼mc�Ż¼ė╔╔Ž╩÷ĮY(ji©”)šō▓╗ļy═Ų│÷ĻP(gu©Īn)ė┌╚²ĮŪą╬╚²ŚlųąŠĆķLĄ─╣½╩ĮŻ«
ĪĪĪĪ═Ųšō Ī„ABCĄ─ųąŠĆķL╣½╩ĮŻ║
ĪĪĪĪ ĪĪ
ĪĪ
ĪĪĪĪ
ĪĪĪĪ ĪĪ
ĪĪ
ĪĪĪĪšf├„ ╚²ĮŪą╬Ą─ųąŠĆīó╚²ĮŪą╬Ęų×ķā╔éĆ╚²ĮŪą╬��Ż¼Ųõųąę╗éĆ╩ŪõJĮŪ╚²ĮŪą╬�����Ż¼┴Ēę╗éĆ╩ŪŌgĮŪ╚²ĮŪą╬(│²Ą╚č³╚²ĮŪą╬═Ō)Ż«└¹ė├ÅV╣┤╣╔Č©└ĒŪĪ║├Ž¹╚źŽÓĘ┤ĒŚ�����Ż¼½@Ą├ųąŠĆ╣½╩ĮŻ«ó┘Īõ�����Ż¼ó┌ĪõŻ¼ó█ĪõųąĄ─ma�����Ż¼mb��Ż¼mcĘųäe▒Ē╩Ša���Ż¼b�Ż¼c▀ģ╔ŽĄ─ųąŠĆķLŻ«
ĪĪĪĪ└²3 ╚ńłD2-23╦∙╩ŠŻ«Ū¾ūCŻ║╚╬ęŌ╦─▀ģą╬╦─Śl▀ģĄ─ŲĮĘĮ║═Ą╚ė┌ī”ĮŪŠĆĄ─ŲĮĘĮ║═╝ėī”ĮŪŠĆųą³c(di©Żn)▀BŠĆŲĮĘĮĄ─4▒ČŻ«

ĪĪĪĪĘų╬÷ ╚ńłD2-23╦∙╩ŠŻ«ī”ĮŪŠĆųą³c(di©Żn)▀BŠĆPQ��Ż¼┐╔┐┤ū„Ī„BDQĄ─ųąŠĆ�����Ż¼└¹ė├└²2Ą─ĮY(ji©”)šō�Ż¼▓╗ļyūC├„▒ŠŅ}Ż«
ĪĪĪĪūC įO(sh©©)╦─▀ģą╬ABCDī”ĮŪŠĆACŻ¼BDųą³c(di©Żn)Ęųäe╩ŪQ���Ż¼PŻ«ė╔└²2�Ż¼į┌Ī„BDQųą�����Ż¼

ĪĪĪĪ╝┤
ĪĪĪĪ2BQ2+2DQ2=4PQ2+BD2Ż« ó┘
ĪĪĪĪį┌Ī„ABCųąŻ¼BQ╩ŪAC▀ģ╔ŽĄ─ųąŠĆ�����Ż¼╦∙ęį
ĪĪĪĪ
ĪĪĪĪį┌Ī„ACDųą�Ż¼QD╩ŪAC▀ģ╔ŽĄ─ųąŠĆŻ¼╦∙ęį
ĪĪĪĪ
ĪĪĪĪīóó┌����Ż¼ó█┤·╚ļó┘Ą├
ĪĪĪĪ
ĪĪĪĪ=4PQ2+BD2Ż¼
ĪĪĪĪ╝┤
AB2+BC2+CD2+DA2=AC2+BD2+4PQ2Ż«
ĪĪĪĪšf├„ ▒ŠŅ}╩Ū└²2Ą─æ¬(y©®ng)ė├Ż«╔Ųė┌īóę¬ĮŌøQĄ─å¢Ņ}▐D(zhu©Żn)╗»×ķęčĮŌøQĄ─å¢Ņ}�Ż¼╩Ū╚╦éāĮŌøQå¢Ņ}Ą─ę╗ĘN╗∙▒ŠĘĮĘ©Ż¼╝┤╗»╬┤ų¬×ķęčų¬Ą─ĘĮĘ©Ż«Ž┬├µ�Ż¼╬ęéāį┘┐┤ā╔éĆ└²Ņ}���Ż¼šf├„▀@ĘN▐D(zhu©Żn)╗»ĘĮĘ©Ą─æ¬(y©®ng)ė├Ż«
ĪĪĪĪ└²4 ╚ńłD2-24╦∙╩ŠŻ«ęčų¬Ī„ABCųą�Ż¼ĪŽC=90ĪŃ����Ż¼DŻ¼EĘųäe╩ŪBC�Ż¼AC╔ŽĄ─╚╬ęŌę╗³c(di©Żn)Ż«Ū¾ūCŻ║AD2+BE2=AB2+DE2Ż«
ĪĪĪĪĘų╬÷ Ū¾ūCųą╦∙╩÷Ą─4ŚlŠĆČ╬Ęųäe╩Ū4éĆų▒ĮŪ╚²ĮŪą╬Ą─ą▒▀ģŻ¼ę“┤╦┐╝æ]Å─╣┤╣╔Č©└Ē╚ļ╩ųŻ«
ĪĪĪĪūC AD2=AC2+CD2Ż¼BE2=BC2+CE2���Ż¼╦∙ęį
ĪĪĪĪAD2+BE2=(AC2+BC2)+(CD2+CE2)=AB2+DE2
ĪĪĪĪ└²5 Ū¾ūCŻ║į┌ų▒ĮŪ╚²ĮŪą╬ųąā╔Ślų▒ĮŪ▀ģ╔ŽĄ─ųąŠĆĄ─ŲĮĘĮ║═Ą─4▒ČĄ╚ė┌ą▒▀ģŲĮĘĮĄ─5▒ČŻ«
ĪĪĪĪ╚ńłD2-25╦∙╩ŠŻ«įO(sh©©)ų▒ĮŪ╚²ĮŪą╬ABCųą�Ż¼ĪŽC=90ĪŃ�����Ż¼AM�Ż¼BNĘųäe╩ŪBCŻ¼AC▀ģ╔ŽĄ─ųąŠĆŻ«Ū¾ūCŻ║
4(AM2+BN2)=5AB2Ż«
ĪĪ

ĪĪĪĪĘų╬÷ ė╔ė┌AM��Ż¼BN���Ż¼ABŠ∙┐╔┐┤ū„─│éĆų▒ĮŪ╚²ĮŪą╬Ą─ą▒▀ģ��Ż¼ę“┤╦����Ż¼Ę┬└²4Ą─ĘĮĘ©┐╔Å─╣┤╣╔Č©└Ē╚ļ╩ų�Ż¼Ą½╚ń╣¹╬ęéā─▄īó▒ŠŅ}┐┤│╔└²4Ą─╠ž╩ŌŪķør©D©D╝┤MŻ¼NĘųäe╩Ū╦∙į┌▀ģĄ─ųą³c(di©Żn)�����Ż¼─Ū├┤┐╔ų▒Įė└¹ė├└²4Ą─ĮY(ji©”)šōŻ¼╩╣ūC├„▀^│╠╩«Ęų║åØŹŻ«
ĪĪĪĪūC ▀BĮėMN����Ż¼└¹ė├└²4Ą─ĮY(ji©”)šōŻ¼╬ęéāėą
AM2+BN2=AB2+MN2��Ż¼
ĪĪĪĪ╦∙ęį 4(AM2+BN2)=4AB2+4MN2Ż« ó┘
ĪĪĪĪė╔ė┌M����Ż¼N╩ŪBCŻ¼ACĄ─ųą³c(di©Żn)��Ż¼╦∙ęį

ĪĪĪĪ╦∙ęį 4MN2=AB2Ż« ó┌
ĪĪĪĪė╔ó┘����Ż¼ó┌
4(AM2+BN2)=5AB2Ż«
ĪĪĪĪšf├„ į┌ūC├„ųąŻ¼ŠĆČ╬MNĘQ×ķĪ„ABCĄ─ųą╬╗ŠĆ�Ż¼ęį║¾Ģ■ų¬Ą└ųą╬╗ŠĆĄ─╗∙▒Šąį┘|(zh©¼)Ż║Ī░MNĪ╬ABŪęMN= łD2-26╦∙╩ŠŻ«MN╩ŪĪ„ABCĄ─ę╗Ślųą╬╗ŠĆŻ¼įO(sh©©)Ī„ABCĄ─├µĘe×ķSŻ«ė╔ė┌M�����Ż¼NĘųäe╩Ū╦∙į┌▀ģĄ─ųą³c(di©Żn)���Ż¼╦∙ęįSĪ„ACM=SĪ„BCN�Ż¼ā╔▀ģ£p╚ź╣½╣▓▓┐ĘųĪ„CMN║¾Ą├SĪ„AMN=SĪ„BMN�Ż¼Å─Č°AB▒ž┼cMNŲĮąąŻ«ėųSĪ„ABM=
łD2-26╦∙╩ŠŻ«MN╩ŪĪ„ABCĄ─ę╗Ślųą╬╗ŠĆŻ¼įO(sh©©)Ī„ABCĄ─├µĘe×ķSŻ«ė╔ė┌M�����Ż¼NĘųäe╩Ū╦∙į┌▀ģĄ─ųą³c(di©Żn)���Ż¼╦∙ęįSĪ„ACM=SĪ„BCN�Ż¼ā╔▀ģ£p╚ź╣½╣▓▓┐ĘųĪ„CMN║¾Ą├SĪ„AMN=SĪ„BMN�Ż¼Å─Č°AB▒ž┼cMNŲĮąąŻ«ėųSĪ„ABM= Ė▀ŽÓ═¼Ż¼Č°SĪ„ABM=2SĪ„BMN����Ż¼╦∙ęįAB=2MNŻ«
Ė▀ŽÓ═¼Ż¼Č°SĪ„ABM=2SĪ„BMN����Ż¼╦∙ęįAB=2MNŻ«

ŠÜ┴Ģ(x©¬)╩«ę╗
ĪĪĪĪ1Ż«ė├Ž┬├µĖ„łD“×ūC╣┤╣╔Č©└Ē(╠ōŠĆ┤·▒Ē▌oų·ŠĆ)Ż║
ĪĪĪĪ(1)┌wŠ²ŪõłD(łD2-27)Ż╗

ĪĪĪĪ(2)ĒŚ├¹▀_(d©ó)łD(2-28)�Ż╗
ĪĪĪĪ(3)ŚŅū„├ČłD(łD2-29)Ż«
ĪĪĪĪ2Ż«ęčų¬Šžą╬ABCDŻ¼P×ķŠžą╬╦∙į┌ŲĮ├µā╚(n©©i)Ą─╚╬ęŌę╗³c(di©Żn)�����Ż¼Ū¾ūCŻ║PA2+PC2=PB2+PD2Ż«

 ĪĪ
ĪĪ
ĪĪĪĪ(╠ß╩ŠŻ║æ¬(y©®ng)Ęų╚²ĘNŪķą╬╝ėęįėæšō�����Ż¼Pį┌Šžą╬ā╚(n©©i)�����ĪóPį┌Šžą╬╔Ž��ĪóPį┌Šžą╬═Ō��Ż¼Š∙ėą▀@éĆĮY(ji©”)šōŻ«)
ĪĪĪĪ3Ż«ė╔Ī„ABCā╚(n©©i)╚╬ęŌę╗³c(di©Żn)OŽ“╚²▀ģBC����Ż¼CA����Ż¼ABĘųäeū„┤╣ŠĆ�����Ż¼┤╣ūŃĘųäe╩ŪD�����Ż¼E�Ż¼FŻ«Ū¾ūCŻ║
AF2+BD2+CE2=FB2+DC2+EA2Ż«
ĪĪĪĪ4Ż«╚ńłD2-30╦∙╩ŠŻ«į┌╦─▀ģą╬ADBCųąŻ¼ī”ĮŪŠĆABĪ═CDŻ«Ū¾ūCŻ║AC2+BD2=AD2+BC2Ż«╦³Ą──µČ©└Ē╩Ūʱ│╔┴ó�Ż┐ūC├„─ŃĄ─ĮY(ji©”)šōŻ«
ĪĪĪĪ5Ż«╚ńłD2-31╦∙╩ŠŻ«Å─õJĮŪ╚²ĮŪą╬ABCĄ─Ēö³c(di©Żn)BŻ¼CĘųäeŽ“?q©▒)”▀ģū„┤╣ŠĆBE�Ż¼CFŻ«Ū¾ūCŻ║
BC2=AB?BF+AC?CEŻ«


ĪĪĪĪ ÜgėŁ╩╣ė├╩ųÖC(j©®)ĪóŲĮ░ÕĄ╚ęŲäėįO(sh©©)éõįLå¢ųą┐╝ŠW(w©Żng)��Ż¼2024ųą┐╝ę╗┬Ę┼Ń░ķ═¼ąą�ŻĪ>>³c(di©Żn)ō¶▓ķ┐┤









